인공지능을 위한 수학

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 수강한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

벡터 Vector

Vector란?

벡터란 숫자를 원소로 가지는 리스트(list) 또는 배열(array)이다.

세로로 나열되어 있을 경우 열벡터, 가로로 나열되어 있을 경우 행벡터라고 부른다.

벡터 내부에 들어있는 원소의 개수는 벡터의 차원이라고 한다.

벡터의 의미

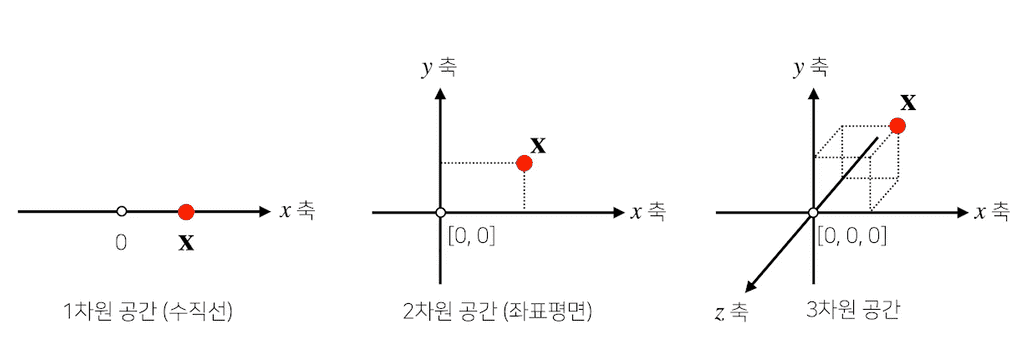
• 공간에서 한 점을 나타낸다.
  • 1차원(수직선 공간)이라면 수직선 위의 한 점
  • 2차원(좌표평면)이라면 좌표평면상의 한 점(x,y)
  • 3차원 공간이라면 공간 상의 한 점(x,y,z)
  • 일반적으로 인공지능에서 다루는 차원은 훨씬 더 큰 경우가 대부분이다.

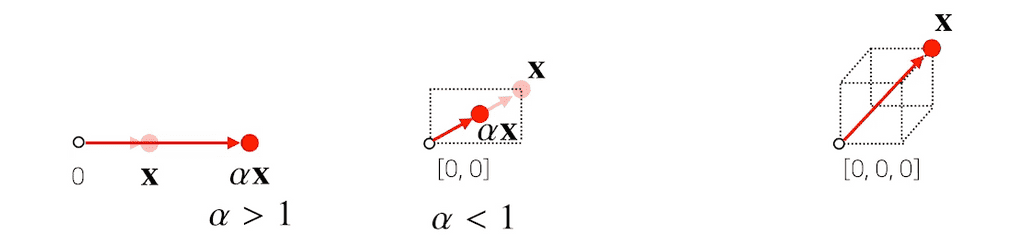
• 원점으로부터의 상대적 위치(화살표)를 표현한다.

  • 이 때, 벡터에 숫자를 곱해주면 길이를 변환할 수 있다. 이를 스칼라곱이라고 부른다.

    TEXT

    Copy

    - 1보다 크면 길이가 늘어나고, 1보다 작으면 길이가 줄어든다.
    - 단, 0보다 작으면 화살표의 방향이 반대로 바뀐다.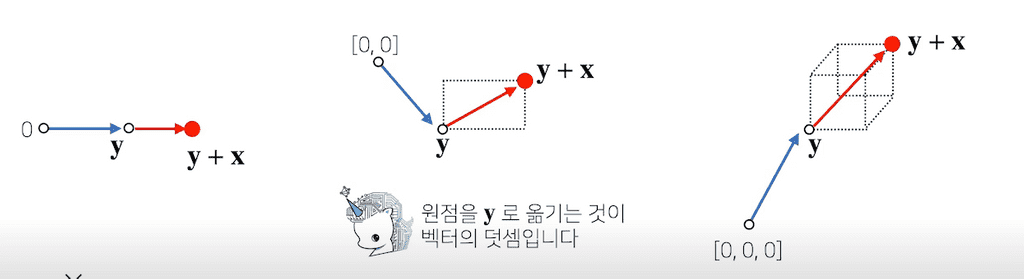

    

  • 두 벡터의 덧셈은 다른 벡터로부터의 상대적 위치이동을 표현한다.

  • 뺄셈은 방향을 뒤집은 덧셈과 같다.

벡터간의 연산

벡터끼리 같은 모양을 가지면...

• 덧셈과 뺄셈을 계산할 수 있다.
• 성분곱(Handamard product)을 계산할 수 있다.
  • 각 벡터의 같은 위치 성분끼리 곱하는것(Numpy의 Element-wise 개념)

따라서 벡터간의 계산 시 차원수를 유의하는 것이 항상 중요하다.

벡터의 노름

벡터의 노름(norm)은 원점으로부터의 거리를 의미한다.

이 때, 거리는 임의의 차원에서 계산할 수 있는 개념이기 때문에, 해당 식은 임의의 차원 d에 대해 성립한다.

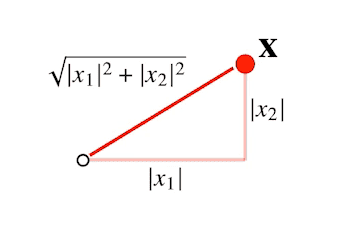
노름은 다음과 같은 두가지 방식으로 구할 수 있다.

• $L_1 노름$ : 각 성분의 변화량의 절대값을 모두 더한것

  $\Vert x \Vert _1 = \displaystyle\sum_{i=1}^d \vert x_i \vert$

  예를 들어, 2차원에서는 x좌표 이동절대값과 y좌표 이동절대값을 모두 더한것을 의미한다.

• $L_2 노름$ : 피타고라스 정리를 이용해 유클리드 거리를 계산한 것

  $\Vert x \Vert _2 = \sqrt{\displaystyle\sum_{i=1}^d {\vert x_i \vert}^2}$

이를 Python으로 구현해보면 다음과 같다.

def l1_norm(x):
    x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm
def l2_norm(x):
    x_norm = x*x
    x_norm = np.sum(x_norm)
    x_nrom = np.sqrt(x_norm)
    return x_norm
# L2 노름은 다음과 같은 np 함수를 사용하여 구할수도 있다.
np.linalg.norm()

그렇다면, 왜 굳이 노름을 구하는 데에 두가지나 방법이 필요한 것일까?

노름의 종류에 따라 기하학적인 성질이 달라지기 때문이다.

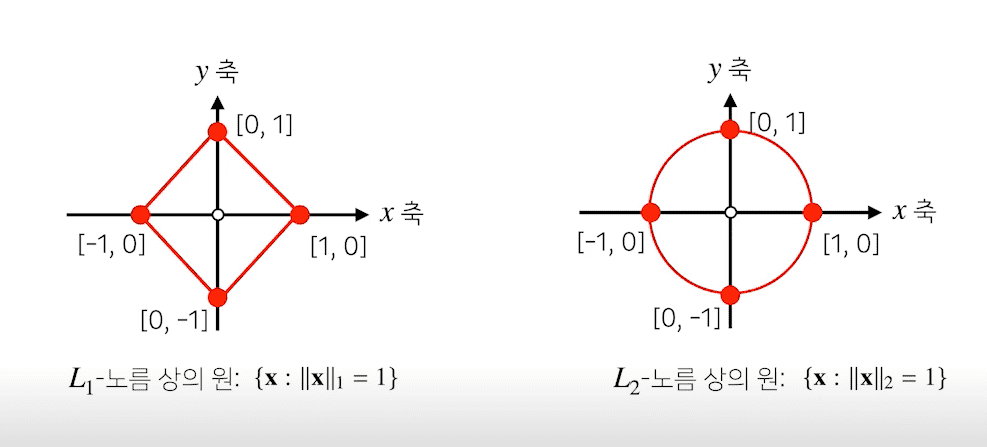
이처럼 두 노름은 성질이 달라 ML에서 어떤 목적으로 사용할 것인지에 따라 선택된다.

L1 노름은 Robust 학습이나 Lasso 회귀에 자주 사용되고, L2 노름은 Laplace 근사, Ridge 회귀에 사용된다.

두 벡터 사이의 거리를 계산하기

두 벡터사이의 거리를 구하는 것은 두 점이 주어졌을 때, 두 점사이의 거리를 구하는 것과 같다.

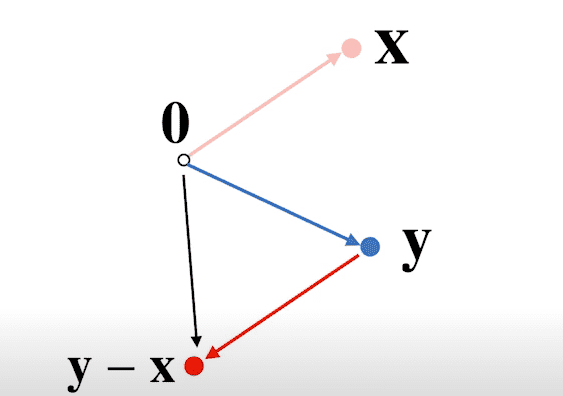
• L1 노름과 L2 노름을 이용한다
• 벡터의 뺄셈을 이용한다.
• 뺄셈을 거꾸로 해도 거리는 같다.
• 원점부터 $\vert x-y\vert$ 까지의 거리가 곧 두 점 사이의 거리이다.

두 벡터 사이의 각도를 구하기

두 벡터 사이의 거리를 이용하여 각도도 계산할 수 있다.

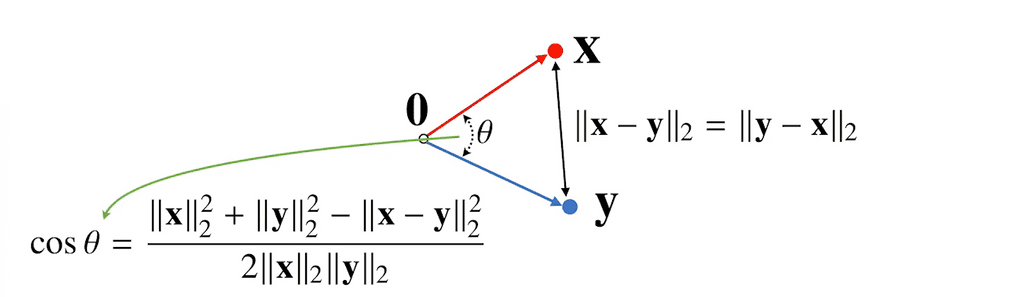
• 제 2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산할 수 있다.
  • $cosB = \frac{a^2+c^2-b^2}{2ac}$
• 2차원 평면이 아니라, 일반화된 d 차원에서도 각도를 계산할 수 있을까?
  • 가능하다. 제 2코사인 법칙을 이용하면 임의의 n 차원에 대해서 각도를 계산할 수 있다.
• 이 때, 분자를 쉽게 계산하는 방법이 내적(inner product)이다.
  • 내적 연산은 np.inner()를 이용하여 쉽게 계산할 수 있다.

이를 Python으로 계산하면 다음과 같다.

def angle(x,y):
    v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

내적은 무엇인가?

내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있다.

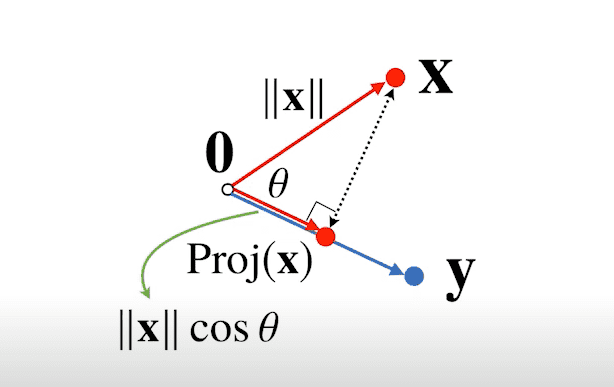
• y 벡터 위에 X 벡터를 정사영한 벡터를 $Proj(x)$라고 하며, 이는 $\Vert x \Vert cos\theta$와 같다.
• 이 때, 내적은 정사영된 길이를 벡터 y의 길이 $\Vert y \Vert$만큼 (곱하여) 조정한 값이다.
• 내적은 두 벡터 사이의 유사도를 측정하는 데에 사용된다.

행렬 Matrix

행렬이란?

행렬은 벡터를 원소로 가지는 2차원 배열을 의미한다.

Numpy 에서 코딩을 할 때는 열벡터가 아니라 행벡터를 기준으로 계산한다.

• 행렬은 행(row)와 열(column)이라는 인덱스를 가진다.
• 행렬의 특정 행을 고정하면 행벡터, 특정 열을 고정하면 열벡터라고 부른다.
• 전치행렬(transpose matrix)는 행과 열의 인덱스가 바뀐 행렬을 말한다.

행렬의 의미

벡터가 공간에서 한 점을 의미한다면, 행렬은 공간에서 여러 점을 나타낸다.

• 행렬의 행벡터 $x_i$는 $i$번째 데이터를 의미한다.
• 행렬의 $x_{ij}$는 $i$번째 데이터의 $j$번째 변수값을 의미한다.

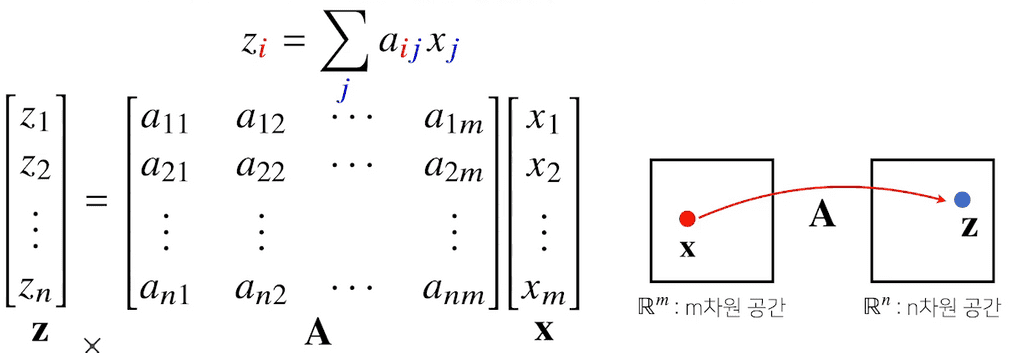
또한, 행렬을 벡터공간에서 사용되는 연산자(operator)로 이해할 수 있다.

• 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
• 이처럼 행렬곱을 통해 패턴을 추출할 수 있고, 데이터를 압축할 수도 있다.
• 이런 행렬곱의 연산자기능을 linear transform, 선형 변환 이라고 말하기도 한다.
  • 딥러닝은 선형 변환과 비선형 함수들의 합성으로 이루어져있다.

행렬간의 연산

행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱

• 행렬은 벡터를 원소로 가지는 2차원 배열이므로, 행렬끼리 같은 모양을 가지면 덧셈과 뺄셈을 계산할 수 있다.
• 성분곱/스칼라곱도 벡터의 성분곱/스칼라곱과 방식이 동일하다.

행렬의 곱셈(matrix multiplication)

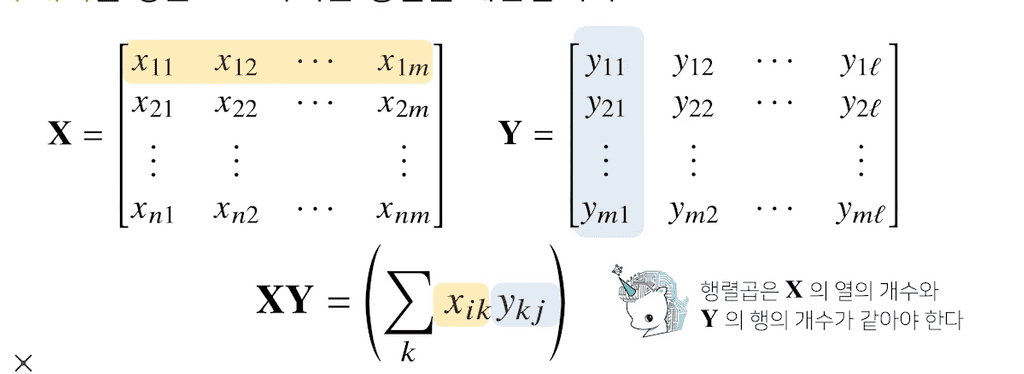
두 행렬 중, 앞 행렬의 $i$번째 행백터와 뒤 행렬의 $j$번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.

따라서 행렬의 곱셈은 X의 열 개수와 Y의 행 개수가 같아야하며, 행렬의 순서과 관계가 있다.

Numpy에서는 @ 을 사용하여 행렬의 곱셈을 계산한다. 이는 np.matmul을 호출하는 연산이다.

이 때, np.dot과 np.matmul은 다른 기능을 가지고 있음에 유의하자.

• dot은 스칼라배가 허용되지만, matmul은 허용되지 않는다.(matrix multiplication이므로)
• 2차원 행렬에서의 곱셈 결과는 동일하지만, 3차원 이상의 행렬곱(tensor multiplication)에서는 다른 결과를 나타낸다.
• 정확히 말하면, np.dot은 두 배열의 내적곱(dot product)이며 matmul은 두 배열의 행렬곱(matrix product)이다.

이에 대한 자세한 설명은 다음 블로그 글을 참고한다. numpy에서 dot과 matmul의 차이

수학에서 벡터는 일반적으로 열벡터를 의미하며, 변화가 되는 대상을 의미한다.
반면, 수학에서 행벡터는 열벡터에 대한 변화행위자이자 함수, 즉 $f()$를 의미한다.
즉, 행벡터는 열벡터를 인자로 받은 뒤 스칼라를 출력하는 함수이다. 이것이 행과 열을 각각 곱해서 더하는 행렬 곱의 의미이다.

행렬의 내적

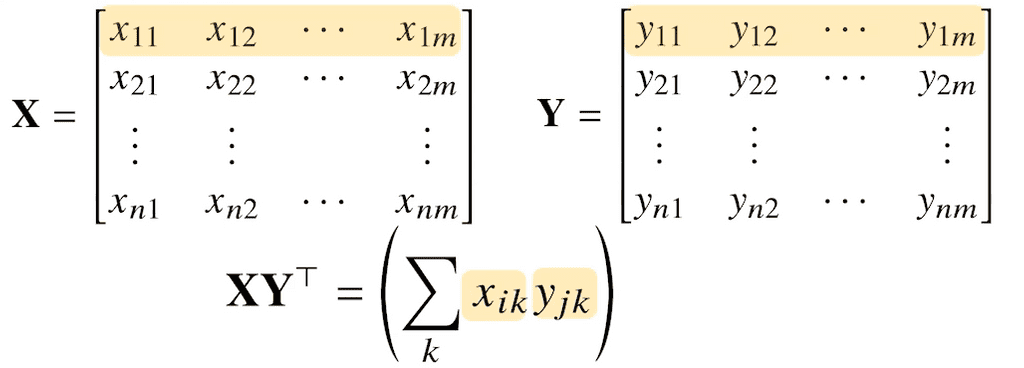
Numpy 의 np.inner() 은 $i$번째 행벡터와 $j$번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.

np.inner는 X @ Y.T의 기능과 같다.

정리하자면, 행렬곱은 Numpy에서 @으로 사용하며, 이는 np.matmul함수를 내부적으로 호출한다.
matmul 함수는 $X$의 행벡터와 $Y$의 열벡터를 내적한다.

행렬 내적은 Numpy에서 np.inner를 사용하여 계산한다.
inner함수는 $X$와 $Y^T$의 행렬곱, 즉 $X$의 행벡터와 $Y$의 행벡터를 내적한다.

내적의 개념이 잘 이해가 되지 않는다면, 다음 블로그를 참조하자.
내적 외에도 선형대수/미적/머신러닝 수학의 설명이 잘 되어있는 블로그이다. 행벡터의 의미와 벡터의 내적 - 공돌이의 수학정리노트

역행렬

어떤 행렬 A를 연산자로 보았을 때, A라는 연산을 거꾸로 되돌리는 연산(행렬)을 역행렬(Inverse Matrix) 이라 부르고, $A^{-1}$로 표기한다.

역행렬은 행(n)과 열(m) 숫자가 같고, 행렬식(determinant)이 0이 아닌 경우에만 계산 가능하다.

Python에서는 np.linalg.inv(M) 함수로 사용가능하며, linalg 는 선형대수(linear algebra)를 의미한다.

X = np.array([[1,2,-3],[7,5,0],[-2,-1,2]])
np.linalg.inv(X) # X의 역행렬
'''
array([[ 0.21276596,  0.0212766 , -0.31914894],
       [-0.29787234,  0.17021277,  0.44680851],
       [ 0.06382979,  0.10638298,  0.40425532]])
'''
X @ np.linalg.inv(X) # X * X의 역행렬 == I(과 근사한 ndarray)
'''
I와 근사한 행렬을 반환한다.(주대각원소를 제외한 나머지 원소들은 0에 가까운 수이다)
array([[ 1.00000000e+00, -1.38777878e-17,  0.00000000e+00],
       [ 0.00000000e+00,  1.00000000e+00,  0.00000000e+00],
       [-2.77555756e-17,  0.00000000e+00,  1.00000000e+00]])
'''

만약 역행렬을 계산할 수 없다면, 유사역행렬(psuedo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $A^+$를 이용한다.

• 단, 이때는 주어진 행렬의 행과 열 중 어느 것의 수가 더 많은지에 따라 계산식이 달라진다.

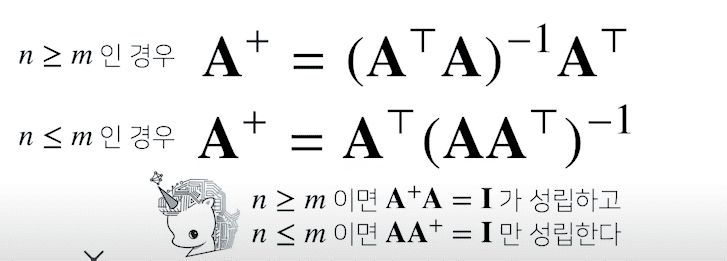
이를 코드로 옮기면 다음과 같다.

Y = np.array([[0,1],[1,-1],[-2,1]]) # 행과 열의 개수가 다르므로 역행렬을 만들 수 없다
np.linalg.pinv(Y) # 유사 역행렬을 만드는 함수
'''
array([[ 5.00000000e-01,  1.11022302e-16, -5.00000000e-01],
       [ 8.33333333e-01, -3.33333333e-01, -1.66666667e-01]])
'''
np.linalg.pinv(Y) @ Y
'''
원래 3x2 행렬이었으나, 유사역행렬은 2x2로 반환되었다(수를 늘리거나 줄여서 반환하기 때문
array([[ 1.00000000e+00, -2.22044605e-16],
       [ 1.11022302e-16,  1.00000000e+00]])
'''

유사역행렬을 구하는 과정에 대해 더 자세하게 알아보고 싶다면 다음 동영상을 참조하자.
Linear Systems of Equations, Least Squares Regression, Pseudoinverse

응용하기 - 연립방정식 해 구하기

np.linalg.pinv 를 이용해 연립방정식의 해를 구할 수 있다.

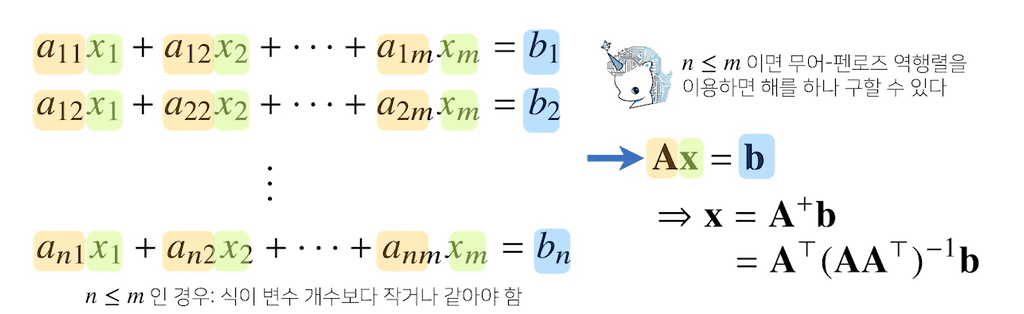
이 때, $(a_{ij})$와 $(b_i)$들이 주어진 상황에서 방정식을 만족하는 $(x_j)$를 구하는 상황이다.

중학교 때 배운 연립 방정식 개념에서, 식의 개수($n$)가 변수의 개수($m$)와 같아야만 해를 구할 수 있었다.
만약, 변수의 개수가 식의 개수보다 많다면 해가 무한히 많거나 부정이 되는데,
그렇게 수많은 해 중 하나를 구하는 것이 유사역행렬을 이용해 구하는 방식이라고 볼 수 있다.

응용하기2 - 선형회귀분석

np.linalg.pinv를 이용하여 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다.

• 선형회귀분석은 연립방정식과 달리, 행이 더 크므로 방정식을 푸는것이 불가능하다. 즉, $X$를 찾는것은 불가능하다.
• 그렇다면 적절한 $\beta$를 찾는 방법은 무엇일까?
• 찾은 선형 모델식을 $\hat{y}$와 실제 값 $y$의 차이($L2-노름$)이 최소화되는 $\beta$를 찾는다.
• Moore-Penrose 역행렬 $X^+$을 $y$ 에 곱해준 값이 곧 $\beta$이다.

# Moore-Penrose 역행렬로 구현하였을 때
# 선형방정식에서 bias항(b)를 표현하기 위해 절편 1을 추가한다. 
# 절편항을 추가하지 않으면, beta의 차원은 1x1이 되는데, 이경우 y=ax가 되어 Y와 X의 방정식이 성립하지 않는다.
X_ = np.array([np.append(x,[1]) for x in x]) # y절편(intercept)항을 직접 추가해주어야한다.
beta = np.linalg.pinv(X_) @ y
y_test = np.append(x, [1]) @ beta

위 코드에서, 왜 절편항을 추가하는지는 포스트 최하단의 풀이를 참고하자.$^{(1)}$

sklearn 의 LinearRegression 을 사용해도 같은 값을 얻을 수 있다.

# Scikit Learn을 활용한 회귀분석
from sklearn.linear_model import LinearRegression
model = LinearRegression() # 선형회귀식
model.fit(X, y)
y_test = model.predict(x_test)

$^{(1)}$

인 $X$와 $Y$가 있다고 하자.

$Y = XA$ 라고 할때, $A$의 차원은 1x1이어야 한다.

따라서 $A = \begin{bmatrix}a\end{bmatrix}$라고 하면,

위와 같은 형태가 되므로,

• 1 = a
• 3 = 2a
• 2 = 3a
• 4 = 4a
• 2 = 5a

즉, $y=ax$형태가 되어 y절편을 구할수가 없다. 이는 선형방정식의 상수항을 표현할 수 없는 결과를 낳는다.

이번엔 intercept항을 추가했을 때를 살펴보자.

$Y = X\_A$ 라고 할때, $A$의 차원은 2x1이어야 한다.

따라서 $A = \begin{bmatrix}a \\b\end{bmatrix}$라고 하면,

위와 같은 형태가 되므로,

• 1 = a + b
• 3 = 2a + b
• 2 = 3a + b
• 4 = 4a + b
• 2 = 5a + b

즉, $y=ax+b$ 형태가 되어 y절편을 표현할 수 있게 된다.

*BoostCamp AI Tech 1기 성예닮 조교님의 풀이를 참고했습니다.