딥러닝의 기초적 이해 - 선형모델부터 역전파에 이르기까지

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 수강한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

딥러닝의 학습방법

선형모델

지난시간까지, 데이터를 선형모델로 해석하여 $y$값과 선형모델 예측값 $\hat{y}$의 차이의 $L2-norm$의 기댓값을 최소화하는 $\beta$를 찾는것이었다.

그러나, 이러한 선형 모델은 단순한 선형문제를 푸는데에는 사용할 수 있겠지만, 분류(classification)이나 더 복잡한 패턴의 문제를 제대로 예측하기가 어렵다.

따라서, 이제부터는 비선형모델인 신경망(Neural Network)를 사용해 보자.

신경망은 비선형모델이지만, 내부적으로는 선형모델들의 결합을 기반으로 만들어져있다.

신경망의 수식 표현

선형 모델

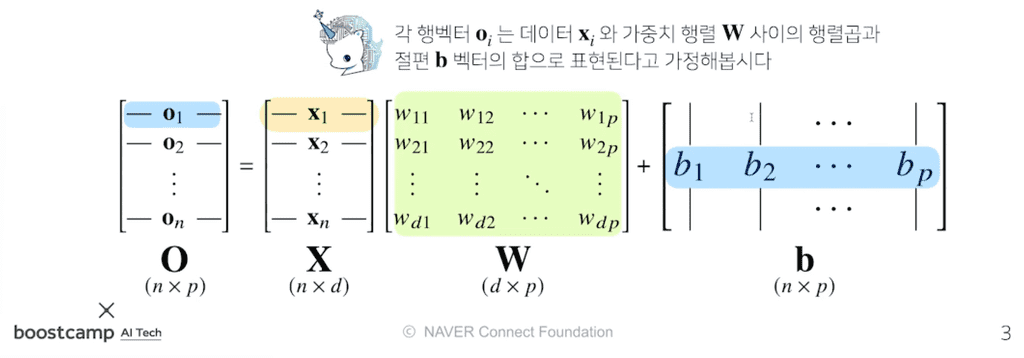
• 전체 데이터가 모인 행렬 $X$
  • $X$의 한 행벡터는 하나의 점으로 표현되는 데이터 포인트이다.
• $X$의 데이터를 출력 $O$로 보내주는 가중치 행렬 $W$
  • $X$의 데이터를 다른 공간으로 보내주는 역할을 한다.
• $y$ 절편에 해당하는 행벡터를 모든 행에 복제하여 만든 절편 행렬 $b$
  • 각 행들은 전부 같은 값 $[b_1, b_2, \cdots, b_p]$를 가진다.

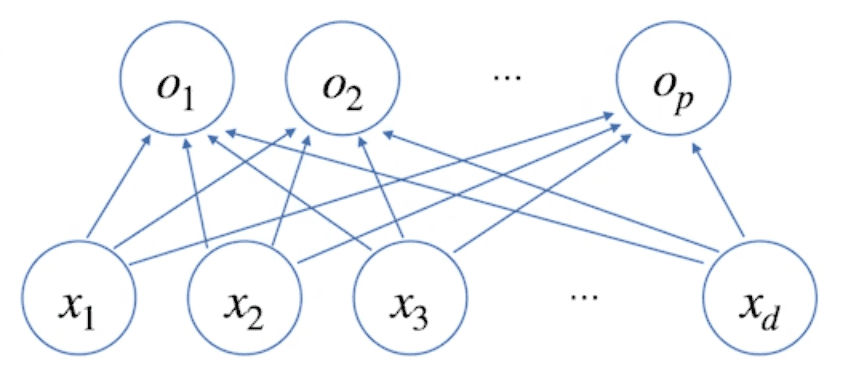
이는 $d$ 개의 변수로 $p$ 개의 선형 모델을 만들어서 $p$ 개의 잠재변수를 설명하는 모델과 동일한 의미이다.

• 위의 그림에서 화살표는 가중치 $W$를 의미한다. 즉, 화살표의 갯수는 $d \times p$ 가 된다.

소프트맥스(softmax) 연산

소프트맥스 함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산이다.

분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측할 수 있다.

$softmax(o) = \left ( \frac{exp(o_1)}{\sum_{k=1}^{p}exp(o_k)}, \cdots , \frac{exp(o_p)}{\sum_{k=1}^{p}exp(o_k)} \right )$

• 선형모델의 출력 $O$ 의 행벡터를 softmax함수의 $o$ 로 집어넣는다.
• softmax 함수는 입력을 확률벡터로 변환시켜 출력한다.
  • 주어진 데이터가 특정 클래스에 속할 확률이 얼마인지를 계산한다.

Python으로 구현한 코드는 다음과 같다.

def softmax(vec):
    # 수식과 달리, np.max값을 취해주는 과정이 추가되어 있다.
    # softmax는 지수함수를 취하므로, 너무 큰 값이 들어왔을 경우 overflow가 생길 위험이 있다.
    # 이를 방지하기 위해 np.max 값을 vector에다 빼 준 뒤 해당 값을 input으로 적용한다.
    denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
    numerator = np.sum(denumerator, axis=-1, keepdims=True)
    val = denumerator / numerator
    return val
vec = np.array([[1,2,0], [-1,0,1], [-10,0,10]])
softmax(vec)
'''
array([[2.44728471e-01, 6.65240956e-01, 9.00305732e-02],
       [9.00305732e-02, 2.44728471e-01, 6.65240956e-01],
       [2.06106005e-09, 4.53978686e-05, 9.99954600e-01]])
[1,2,0]이 [0.24, 0.67, 0.09]라는 확률벡터로 바뀌었다.
'''

왜 분류문제에 있어서 최종 출력값이 확률값이 되어야하고, 소프트맥스 함수를 사용해야 하는지에 대해서는 다음 링크를 참고한다.

해커에게 전해들은 머신러닝 #3

단, 소프트맥스 함수는 학습 시에만 사용하고, 추론을 할 때에는 사용하지 않는다.

추론을 할 때에는 출력값에서 최댓값을 가진 주소만 1로 출력하는 원-핫(one-hot) 벡터를 사용하여, 주어진 출력 중 최댓값 주소만 가져가는 형태로 구현하기 때문이다.

선형함수에 소프트맥스 함수를 적용시켜 선형 모델을 분류문제에 알맞은 확률 추측 모델로 바꾸었듯이 함수를 합성하여 출력값을 조정할 수 있다면, , 선형 함수에 다른 함수를 합성하면 비선형 문제도 풀 수 있지 않을까?

활성함수(activation function)

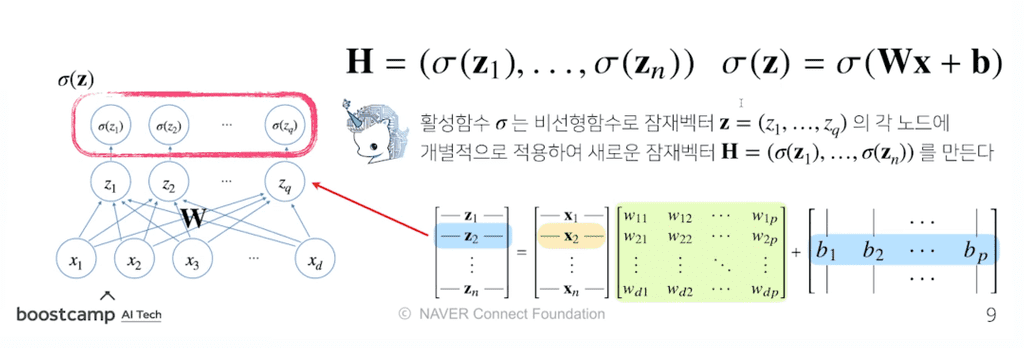
활성함수는 실수값을 입력으로 받아서 다시 실수값으로 뱉는 비선형(nonlinear) 함수이다.

이를 $\mathbb{R}$ 위에 정의된 비선형함수라고 하며, 딥러닝에서 매우 중요한 개념이다.

• 선형모델을 입력으로 받아서 각각의 원소에 대하여 적용된다.
• 정확히 말하면, 활성함수 $\sigma$는 비선형 함수로, 입력 잠재벡터 $\bold{z} = (z_1,\cdots,z_q)$의 각 노드에 개별적으로 적용하여 새로운 잠재 벡터 $\bold{H} = (\sigma(z_1),\cdots,\sigma(z_n))$을 만든다.
  • 이 잠재벡터 $H$를 히든(Hidden) 벡터 또는 뉴런(Neuron)이라 부르기도 한다.
  • 이런 뉴런의 집합체를 신경망, Neural Network라고 부르는 것이다.
• 선형 모델에 활성함수를 한차례 씌워 비선형 모델로 전환한 이런 기본적인 신경망을 역사적으로 퍼셉트론(Perceptron)이라고 부른다.

무엇보다 명심해야할 점은, 활성함수를 쓰지 않으면 딥러닝은 선형모델과 차이가 없다는 것이다.

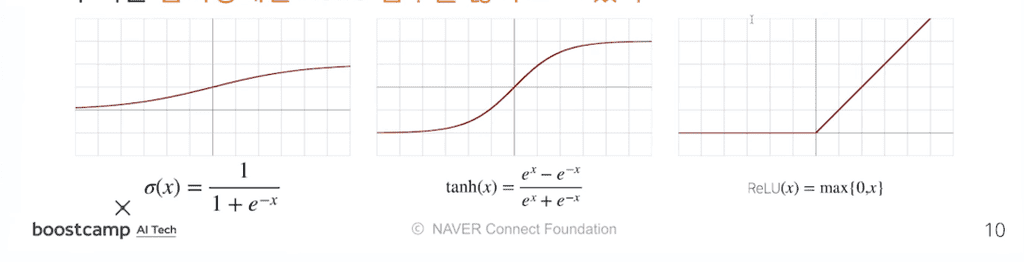
과거에는 활성함수로 시그모이드(sigmoid) 함수나 하이퍼볼릭탄젠트(tanh) 함수를 많이 사용되었으며, 70년정도 된 신경망과 퍼셉트론의 역사에서 큰 역할을 했다.

그러나 오늘날 딥러닝에 가장 많이 쓰이는 함수는 ReLU 함수로, 언뜻 보면 선형함수처럼 보이지만 전형적인 비선형함수이며 비선형함수로서의 좋은 성질들을 많이 가지고 있다.

왜 ReLU 함수가 시그모이드, tanh 함수보다 나은지에 대해서는 다음 링크를 참조하자.

What are the advantages of ReLU over sigmoid function in deep neural networks?

딥러닝에서 사용하는 활성화함수

요약하자면 다음과 같다.

• 시그모이드 함수와 tanh 함수는, Gradient Vanishing 가능성이 비교적 높다.
  • 시그모이드 함수는 미분값(gradient 값)의 최대가 $\frac{1}{4}(x=0)$ 밖에 되지 않고, 어느 정도 input값이 올라가면 거의 0에 수렴한다. 이 경우 $|x|$값이 커질수록 backpropagation 과정에서 미분값이 소실될 가능성이 크다.
  • tanh 함수도 비슷한 문제가 있다.
• 시그모이드 함수는 함수값 중심이 0이 아니다.
  • 모든 파라미터의 미분값이 같은 부호를 가지게 되어, 같은 방향으로 update되게 된다.
  • 이는 학습을 지그재그형태로 만들어 학습이 느려지는 원인이 된다.
• 시그모이드 함수는 exp 함수 사용시 비용이 크다.

신경망

신경망은 선형모델과 활성함수를 합성한 함수이다.

위에서 짚었던 활성함수 개념을 토대로, 신경망을 층층이 만들어 보자.

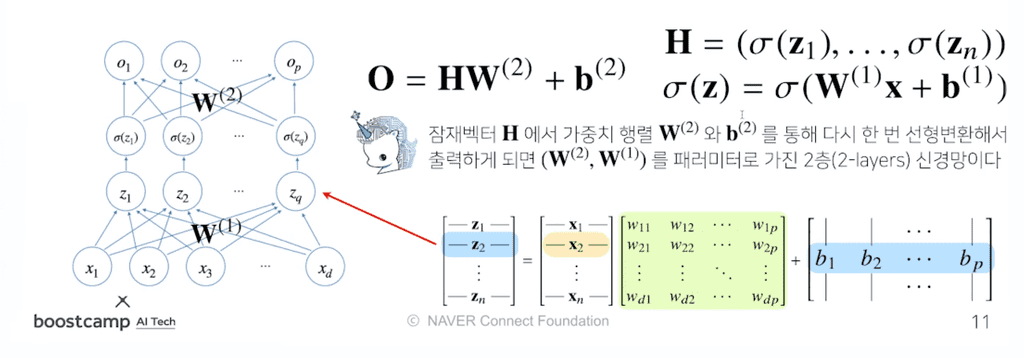
2층 신경망(2-layer NN) 구현하기

1. $X$를 가중치 행렬 $W^{(1)}$와 $b^{(1)}$로 선형변환시켜 $Z$라는 출력을 받는다.
2. $Z$에 활성함수 $\sigma$를 씌워서 히든벡터 $H$를 만든다. - 이 때 활성함수는 Z의 각 원소$z_k$에 개별적으로 적용된다.
3. 히든 벡터 $H$를 다시 가중치 행렬 $W^{(2)}$와 $b^{(2)}$를 통해 선형변환해서 출력한다.

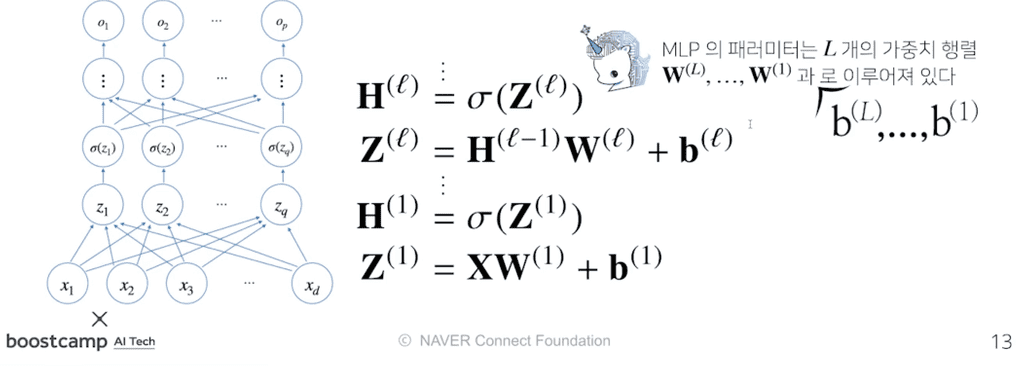
다층(multi-layer) 퍼셉트론, MLP는 이처럼 [선형변환 - 활성함수 합성] 사이클을 n회 반복하여 신경망이 여러층 합성된 함수이다.

• MLP의 파라미터는 $L$개의 가중치 행렬 $W^{(L)},\dots,W^{(1)}$과 $y$절편 $b^{(L)},\dots,b^{(1)}$로 이루어져 있다.
• 이 때 $\ell = 1,\dots,L$ 까지의 순차적인 신경망 계산을 순전파(forward propagation)이라고 부른다.

층을 여러개 쌓는 이유

이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있다.

• 이를 universal approximation theorem이라고 한다.

그러나 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능하다. 즉, 바꾸어 말하면 적은 수의 뉴런으로도 층을 더 깊게 쌓으면 훨씬 더 복잡한 함수를 표현할 수 있다.

• 층이 얇으면 필요한 뉴런의 숫자가 기하급수적으로 늘어나, 넓은(wide) 신경망이 되어야한다.

딥러닝의 학습 원리

역전파 알고리즘

앞서 말했던 순전파(forward propagation)는 입력값 $X$를 받아서 선형모델과 활성함수를 반복적으로 적용하여 출력하는 연산이었다.

이 때, 가중치 $W$를 학습시키려면 각각의 가중치에 대한 gradient 벡터를 계산해야한다.

• 이는 선형회귀에서의 경사하강법에서 $\beta$를 구하던 것과 같은 개념이다.

이 과정을 역전파(backpropagation) 알고리즘으로 수행한다.

• 각 층에 존재하는 파라미터들에 대한 미분을 계산해서, 그 미분 값을 가지고 파라미터를 업데이트한다.

가중치를 업데이트할 때, 행렬의 모든 원소개수만큼, 또 $y$절편의 모든 원소 개수만큼 경사하강법이 적용된다. 따라서 기존의 선형모델보다 훨씬 더 많은 파라미터들에 대해 경사하강법을 적용하게 된다.

또, 선형모델은 한 층에 대해서만 계산하는 모델이므로 gradient 벡터를 한번에 계산할 수 있었지만, 딥러닝은 여러 층에 걸쳐 순차적으로 계산하기 때문에 gradient 벡터를 한번에 계산할 수 없다.

따라서 역전파 알고리즘은 순전파와 비슷하게 역순차적으로 층마다 미분을 계산하여 적용시킨다.

역전파 알고리즘 원리 이해하기

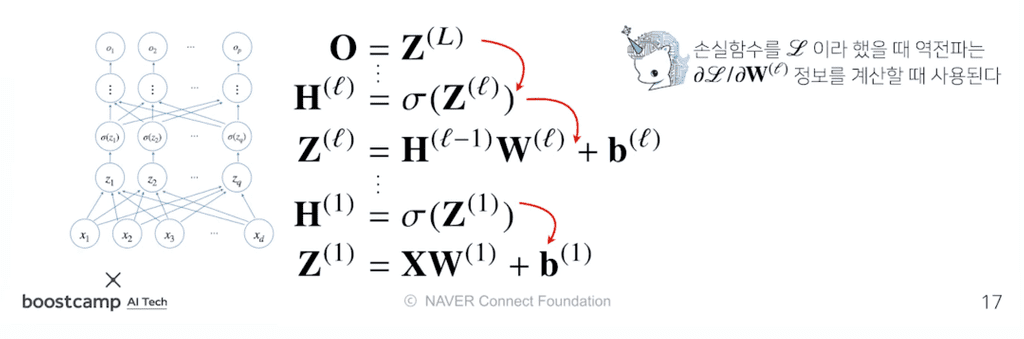
손실함수를 $\mathscr{L}$이라고 했을 때, 각각의 가중치 행렬 $W^{(\mathscr{L})}$마다 손실함수에 대한 미분을 계산할 때 역전파 알고리즘을 사용한다.

• 이 때, 각 층에서 계산된 gradient 벡터들은 밑의 층으로 전달되는 flow 형태이다.
  • 저층에 있는 gradient 벡터를 계산할 때는 위층에 있는 gradient 벡터가 필요하다.
• 즉, 위층에서 아래층으로 내려오면서 업데이트하는 방식이다.

이 원리를 사용할 때 합성함수의 미분법인 연쇄법칙을 사용하여 gradient 벡터를 전달한다.

연쇄법칙(chain-rule)은 합성함수를 미분하는 방식이다. 오늘날의 딥러닝 프레임워크들은 이러한 연쇄법칙을 기반으로 한 자동 미분(auto-differentiation)을 수행하여 신경망을 학습시킨다.

연쇄법칙 예제

위와 같은 함수가 있을 때, $z$를 $x$에 대해서 어떻게 미분할 수 있는가?

일단, 위의 함수를 다음과 같이 두 함수의 결합으로 표현할 수 있다.

이 함수들을 토대로 다음과 같이 연쇄적인 미분값의 곱으로 $\frac{\partial z}{\partial x}$를 표현할 수 있다.

위의 식의 두 미분값을 따로 떼내어 두 함수에 적용시키면 다음과 같다.

이 두 미분값의 곱, $2w \cdot 1 = 2(x+y)$이 $z$의 $x$에 대한 미분값이다.

위와 같은 합성함수미분의 연쇄법칙 과정을 역전파에 적용시킬 수 있다.

2층 신경망 예제

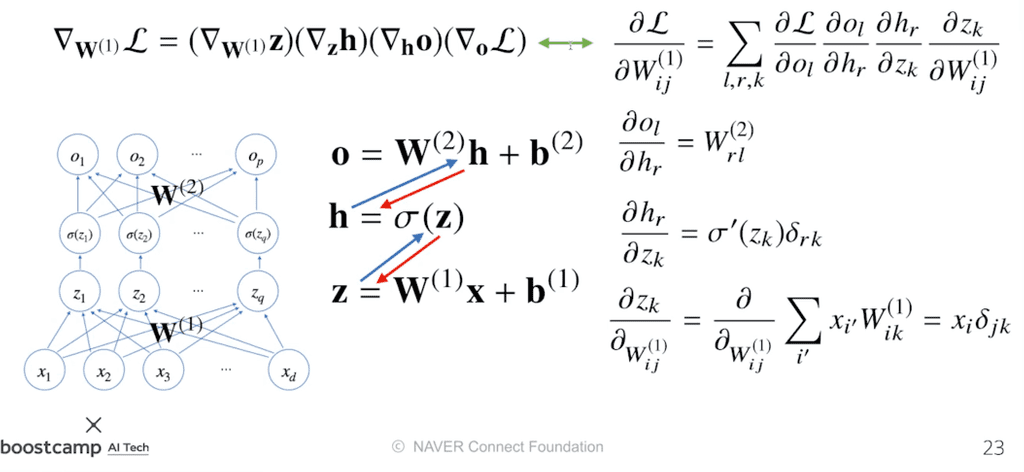
위에서 배운 연쇄법칙을 이용하여 2층 신경망에서의 역전파 과정을 수식으로 정리해볼 수 있다.

위의 그림에서, 파란 화살표는 순전파, 빨간 화살표는 역전파를 의미한다.

첫번째 층에 해당하는 $W^{(1)}$에 대해서 경사하강법을 사용하고 싶을 때, 어떻게 gradient 벡터를 계산하는가?

• $W^{(1)}$은 행렬이므로 각 성분에 대한 편미분을 계산해주어야한다.

각각의 연쇄법칙을 순서대로 적용할 때, 미분값이 각 층마다 계산되므로, 경사하강법에서 실제 가중치 행렬 $W^{(1)}$에 적용시킬 gradient 벡터를 찾아낼 수 있다.

딥러닝을 학습시킬때는 이렇게 계산한 각각의 가중치 행렬에 대한 gradient 벡터를 SGD에 이용하여, 데이터를 바꾸어가면서(mini batch) 파라미터들을 학습시킨다. 이로써 주어진 목적식을 최소화하는 파라미터들을 찾을 수 있다.

레퍼런스

순전파와 역전파의 개념을 좀 더 명확히 알고싶다면, 다음 레퍼런스를 참고하자.

4.7. Forward Propagation, Backward Propagation, and Computational Graphs - Dive into Deep Learning 0.16.1 documentation

3.14. 순전파(forward propagation), 역전파(back propagation), 연산 그래프 - Dive into Deep Learning documentation