딥러닝 베이직 - 03.최적화 기법

BoostCamp AI Tech

Optimization

Generalization

Over-fitting

Cross-validation

Momentum

Adagrad

Adam

Regularization

02/02/2021

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

Optimization

용어 정리

Generalization

많은 경우에 일반화 성능을 높이는 것이 학습의 목적이 된다.

Generalization Gap은 학습오류(Training Error)와 테스트오류(Test Error)사이의 간극을 의미한다. 좋은 일반화 성능(Generalization Performace)이 보장되어있다는 것은 이 갭이 작다는 말이다. 이는 곧, 해당 모델의 (테스트 데이터에 대한) 성능이 학습데이터와 비슷할 것임을 나타낸다.

그런데, 학습 데이터의 자체가 좋지 않아 모델의 성능이 떨어지는 경우가 있을수도 있다. 이 경우에도 학습 데이터와 테스트 데이터의 차이가 적다면 일반화 성능은 좋다고 표현한다. 따라서, 일반화 성능이 좋다고해서 모델의 성능이 좋다는 것을 의미하지는 않는다.

Under-fitting vs over-fitting

오버피팅(Overfitting, 과적합)은 학습 데이터에 대해서는 잘 동작하지만, 테스트 데이터에는 잘 동작하지 않는 것을 의미한다.

반대로, 언더피팅(Underfitting, 과소적합)은 모델의 구성이 너무 간단하거나 학습을 너무 적게 해서 학습 데이터도 잘 맞추지 못하는 것을 의미한다.

이는 개념적인 이야기라서, 해당 모델이 오버피팅/언더피팅임을 판단하는 기준은 절대적이지 않다.

Cross-validation

데이터를 분리하여, 학습데이터는 학습만, 테스트 데이터는 모델의 성능을 테스트하는 validation만 수행한다.

교차검증(Cross-validation)은 학습데이터와 테스트 데이터를 분리하여 검증하는 기술을 의미하는데, 가장 대표적인 것으로 k-fold validation이 있다.

K-fold validation은 테스트 데이터를 제외한 학습 데이터를 k개로 나누어서, k-1개로 학습을 시키고 나머지 한 개로 validation을 하는 기법이다. 이 때 성능을 제대로 검증하기 위해 validation으로 사용하는 하나를 매번 바꿔가며 테스트해본다.

신경망은 최적의 파라미터를 구하기 위한 학습과정에서 하이퍼파라미터(Hyperparameter)가 필요하다.

파라미터
- 가중치와 bias, CNN의 필터 등
- 구하고자 하는 값들
하이퍼파라미터
- 학습률(learning rate), 손실함수(loss function), 신경망의 크기 등
- 직접 정하는 값들

처음에는 어떤 하이퍼파라미터가 좋은지 모르기 때문에, 교차검증으로 하이퍼파라미터를 먼저 찾고나서 모든 학습 데이터를 사용해 파라미터를 구한다.

테스트 데이터는 절대로 학습에 사용하지 않는다. 테스트 데이터는 오로지 테스트만을 위해 사용할 뿐, 학습에 사용되는 것은 그 자체로 cheating으로 본다.

Bias-variance tradeoff

bias-and-variance

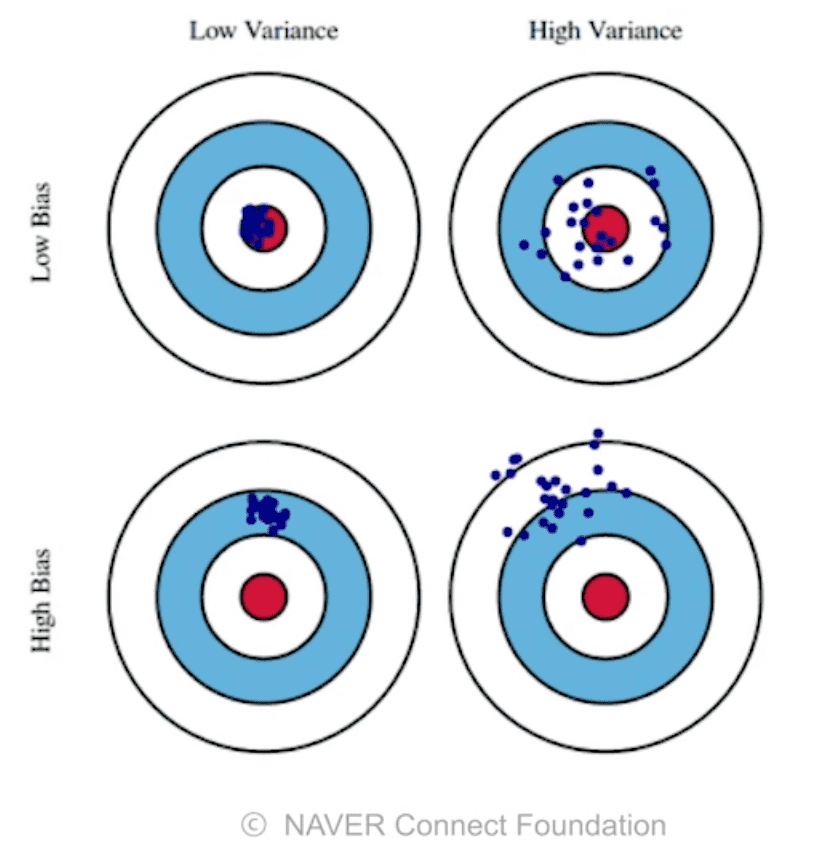
분산(Variance)은 input을 넣었을 때 얼마나 output이 일관적으로 나오는가를 나타낸다. 일반적으로 Variance가 낮은 모델들은 간단한 모델들이다. 이에 비해 Variance가 높은 모델들은 input에 따라 output이 비교적 크게 바뀌므로, 오버피팅될 가능성이 높다.

사격에서의 탄착군 형성을 생각해보자. 중요한 것은 과녁 중심을 얼마나 맞히느냐가 아니라 탄착지점이 얼마나 모여있느냐이다. 탄착군이 모여있으면, 가늠쇠를 조정하여 탄착군을 과녁 중앙으로 shift하면 된다.

편향(Bias)은 분산과 관계없이, 평균값이 목표치(True Target), 즉 정답에 얼마나 접근했는가를 나타낸다. 탄착군이 형성되지 않더라도, 점들의 평균치가 과녁 중앙에 가까이 갔다면 편향이 낮은 것이다.

\textrm{Given}\ D = \{(x_i,t_i)\}^N_{i=1}, \quad\textrm{Where}\quad t = f(x) + \epsilon \quad \textrm{and} \quad \epsilon \sim \mathcal{N}(0,\sigma^2)

Bias and Variance의 트레이드오프 관계는 오래된 주제이다. 아래의 식은 학습데이터에 노이즈가 껴 있음을 가정하고 있다.

\begin{aligned} \mathbb{E}\Big[(t-\hat{f})^2\Big] &= \mathbb{E}\Big[(t-f+f-\hat{f})^2\Big]\\ &= \dots\\ &= \mathbb{E}\Big[(f-\mathbb{E}[\hat{f}])^2\Big] + \mathbb{E}\Big[(\mathbb{E}[\hat{f}]-\hat{f})^2\Big]+\mathbb{E}[\epsilon] \end{aligned}

$t$ 는 True Target, 즉 목표치(정답)을 의미한다.
첫 식은 cost를 의미한다.
마지막 식에서 각 항은 왼쪽부터 차례대로 bias $^2$ , variance, noise를 의미한다.

Cost를 최소화하기 위해 총 세 파트, [bias $^2$ , variance, noise]를 줄여야하는데, 이 중 bias와 variance는 한 쪽을 줄이면 다른 한 쪽이 늘어나는 관계이다. 근본적으로 둘 모두를 줄이기는 힘들다는 fundamental이 존재한다.

Bootstrapping

'부츠 끈을 들어서 하늘을 날겠다'라는 의미의 bootstrap라는 어원에서 유래하였다. '지금 가지고 있는 것으로 어떻게든 활용하여 해결하겠다'라고 볼 수 있는데, 통계학에서는 가설검증이나 metric 계산 이전에 랜덤샘플링을 적용하는 방법을 일컫는다.

서로 다른 학습데이터를 사용했을 때 모델의 예측은 차이가 나게 되는데, 이 예측의 통계(또는 일치도)를 보고 전체적인 모델의 불확실성(uncertainty)를 예측하고자 할 때 부트스트래핑을 사용한다.

여러가지로 활용될 수 있지만, 일반적으로는 학습데이터가 고정되어있을 때 서브샘플링을 통해 여러 학습데이터를 만들고 여러 모델과 metric을 만들어 사용하겠다는 말이다.

Bagging and Boosting

bootstrapping-boosting

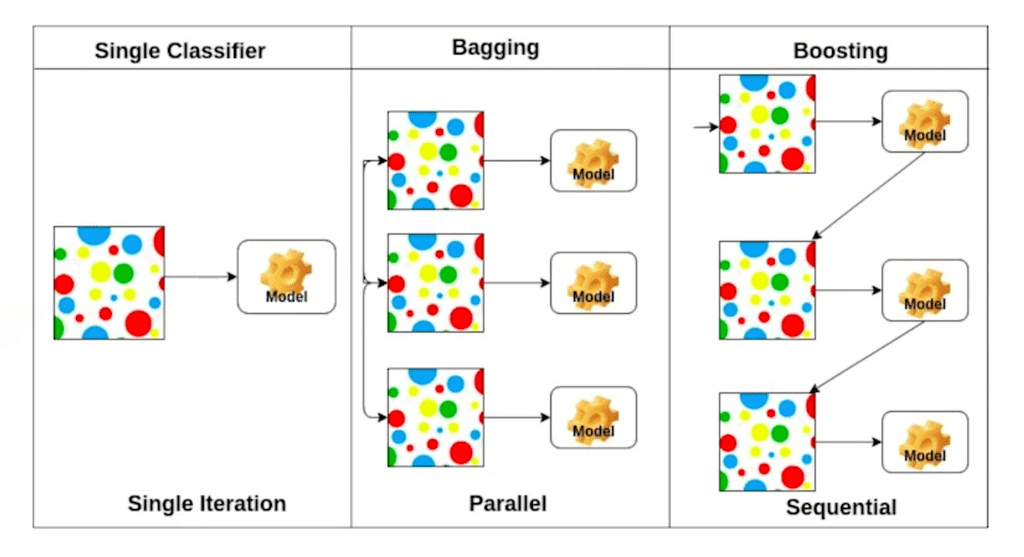
Bagging(Bootstrapping aggregating)은 학습데이터가 고정되어있을 때, 학습데이터를 다 사용하는 것이 아니라 랜덤샘플링한 여러개로 만들어 여러개의 모델을 만든 뒤 이 모델들의 output을 평균낸다는 것을 의미한다. 부트스트래핑과 관련있는 말이며, 앙상블(Ensemble)이라고 불리기도 한다.

직관적으로는 모든 데이터를 학습데이터로 썼을 때 가장 좋은 성능의 모델이 나올 것 같지만, 실제로는 오히려 데이터들을 서브샘플링 한 뒤 여러 모델의 예측을 평균낸 것이 더 성능이 좋은 경우가 많다.

Boosting은 조금 다른 방법이다.

학습데이터를 여러 개로 샘플링한 뒤, 하나의 모델을 가지고 각 샘플링 데이터들을 차례대로 학습시킨다. 해당 모델이 제대로 예측하지 못하는 데이터들에 대해서는, 해당 데이터들만 따로 학습시키는 모델을 새로 만든다. 이 개개의 모델들을 weak learner라고 부른다.

이렇게 여러개의 모델을 만든 뒤 sequential하게 합쳐서 하나의 strong learner를 만드는 것을 부스팅이라고 한다.

Practical Gradient Descent Method

경사하강법 - 배치 방식에 따라

Stochastic Gradient Descent(SGD)
- 한번에 하나의 샘플로만 gradient를 구해서 업데이트하는 방식
Mini-batch Gradient Descent
- 한번에 데이터의 일부(일반적으로 배치 사이즈)로 gradient를 구해서 업데이트하는 방식
- 가장 많이 사용하는 방식
Batch Gradient Descent
- 한번에 모든 데이터로 gradient를 구해서 업데이트하는 방식

배치사이즈는 얼마나 커야하는가?

batch-size

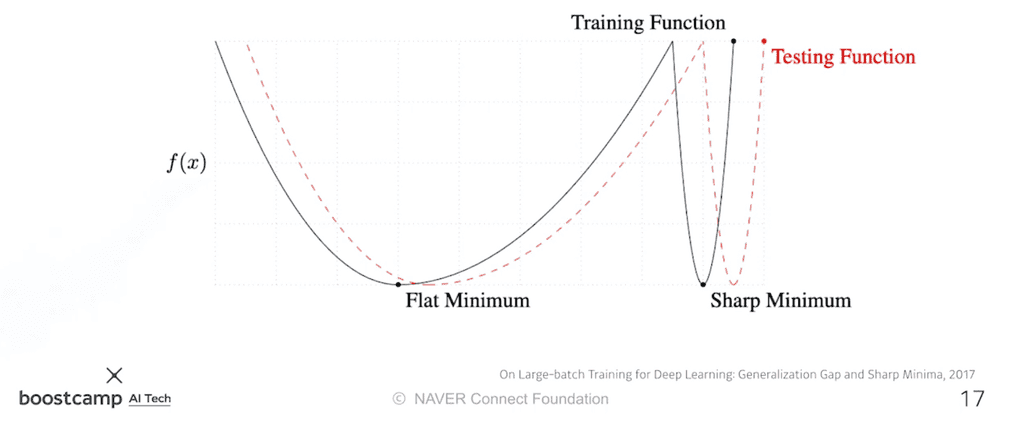
몇몇 논문의 실험 결과 배치사이즈가 너무 커지면 Sharp Minimum에 빠지게 되고, 이는 곧 테스트 데이터에 대한 좋지 않은 성능으로 연결된다는 것이 밝혀졌다.

반대로, 배치사이즈가 작을수록 noise의 영향력이 커지므로 Sharp Minimum에서 탈출할 확률이 높다.

해당 실험을 다룬 On Large-batch Training for Deep Learning : Generalization Gap and Sharp Minima, 2017 논문을 참조해보자.

자세한 설명은 아래 글을 참조한다.

Small Batch Size in Deep Learning

Gradient Descent Methods

(Stochastic) Gradient Descent
- 가장 기본적인 경사하강법
- learning rate를 정하는 것이 어렵다.
Momentum
- 관성처럼, 이전 배치에서의 방향성을 어느정도 유지하는 방식
- 모멘텀 $\beta$ 과 현재 gradient $g$ 를 합친 accumulation를 이용해 업데이트한다.
- gradient가 요동치더라도 이전의 관성이 남아있기 때문에 어느정도 학습이 잘 된다.
Nesterov Accelerated Gradient(NAG)
- Lookahead gradient를 계산한다.
- 기존의 모멘텀은 관성으로 인해 local minimum 부근에서 수렴(converging)하지 못하는 문제가 있었지만, NAG는 모멘텀으로 업데이트 시 발생하는 변화를 미리 체크한 뒤 모멘텀을 결정하므로 좀 더 minimum에 빠르게 수렴할 수 있다.
Adagrad
- 이전까지의 모멘텀방식과 다른 ADA(adaptive) 방식
- $G$ 에 지금까지의 gradient 제곱 합을 저장시키고, 역수에 집어넣는다. 따라서 많이 변한 파라미터는 적게 변화하게되고, 적게 변한 파라미터는 많이 변화하게 된다.
- $G$ 가 계속 커지기 때문에, 분모가 점점 커지므로 learning rate가 0에 수렴해 학습이 멈춘다는 문제가 있다.
Adadelta
- Adagrad에서 $G$ $G$ 가 계속 커지는 문제를 exponential moving average를 통해 해결하려는 방식
  - 지수이동평균은 최근 데이터에 가중치를 부여하고, 과거의 데이터일수록 영향력이 작아지는 형태를 띈다.
  - 단, Adadelta에서는 윈도우사이즈만큼의 local average를 구한다.
- 시간을 기준으로 window를 잡아, 최근에 gradient가 많이 변했으면 적게 변화시키고, 적게 변화했으면 많이 변화시킨다.
- 윈도우 사이즈만큼의 gradient 정보를 들고 있어야하는데, GPT-3같은 천억개 수준의 파라미터를 가진 모델의 정보를 다 들고 있을 수 없다는 문제가 있다.
- learning rate가 없다는 특징이 있는데, 이 때문에 변화를 주기가 어려우므로 잘 사용되지 않는다.
RMSprop
- 제프리 힌턴이 딥러닝 강의를 하다가 언급했던 경험을 바탕으로 구현한 방식
- adadelta처럼 exponential moving average를 이용하지만, 대신 분자에 $\eta$ 라는 stepsize(learning rate)를 넣는다.
- adagrad랑 adadelta랑 섞어놓은 듯한, 과거에 많이 사용되었던 방식이다.
Adam
- Adaptive와 Momentum 방식들을 합친 것으로, 가장 많이 사용하는 방식이다.
- 모멘텀 $m$ 과 gradient 제곱 값들의 합 $v$ 을 사용한다.
- $\epsilon$ $ϵ$ 은 division by zero를 막기 위한 하이퍼파라미터인데, 아주 작은 값을 넣는다. 실제로는 이 값을 잘 조정하는것이 practical한 성능에 큰 영향을 주는 것으로 나타났다.
  - 0이 아니면서 0에 얼마나 가깝게 만드는가?

더 자세한 설명은 다음 글을 참조하자.

Gradient Descent Optimization Algorithms 정리

Regularization

학습을 방해하도록 규제함으로써, 모델이 학습 데이터에만 피팅되는것이 아니라 테스트 데이터에서도 잘 동작하도록 만드는 것, 즉 오버피팅을 피하도록 하는 것을 정규화(regularization)이라고 한다.

Early Stopping

early-stopping

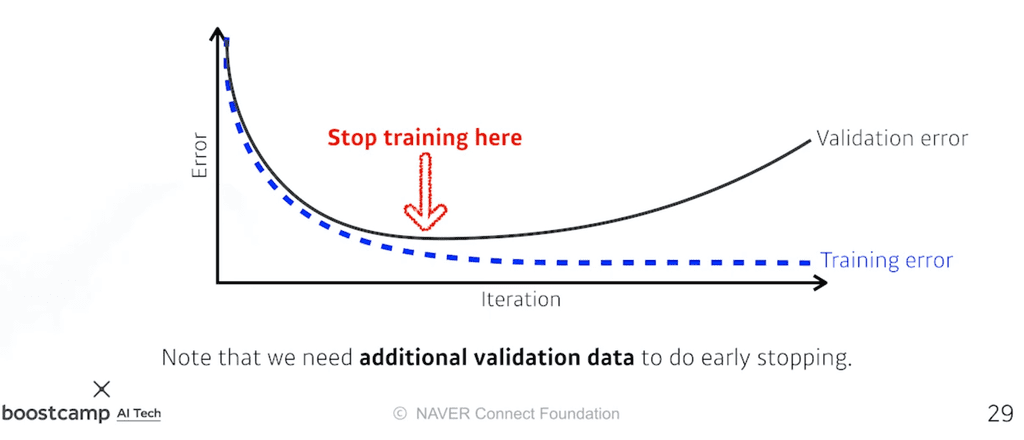
validation 에러와 학습 에러의 차이가 날 정도로 학습하기 전에 학습을 멈추어 버리는것을 Early stopping이라고 한다.

Parameter Norm Penalty

Parameter Norm Penalty는 신경망의 파라미터가 너무 커지지 않도록 조절하는 것을 의미한다.

신경망 파라미터의 숫자들이 너무 커지지 않도록 하기 위해 파라미터 값들(의 제곱의 합)을 줄여준다.

파라미터의 크기가 크지않은, 즉 부드러운(smooth) 함수일수록 일반화성능(Generalization Performance)이 좋을것이라는 가정에 기초하고 있다.

Data Augmentation

data-augmentation

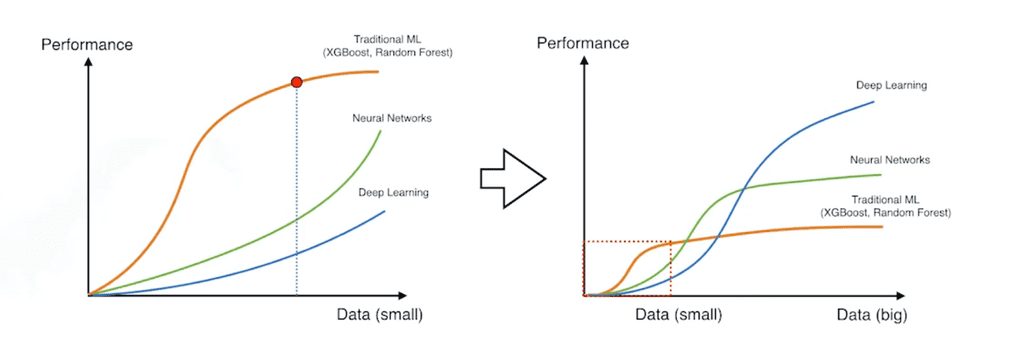
일반적으로 데이터가 많으면 모델의 성능이 더 좋다. 거꾸로 말하면, 데이터가 없으면 딥러닝 모델은 다른 머신러닝 방법론에 비하여 열등하다.

그러나 데이터셋이 어느정도 커지게 되면, 딥러닝 모델은 기존의 머신러닝 방법론들이 따라갈 수 없는 표현력을 가지게 된다. 결국 관건은 데이터의 양이다.

Data Augmentation은 어떤 식으로든 내가 가지고 있는 데이터를 변형시켜서 데이터 풀을 늘리는 방법을 의미한다. 단, 변화는 이미지의 레이블이 바뀌지 않는 한도 내에서 수행해야한다.

예를 들어, MNIST 데이터에서 6을 변형시키겠다고 뒤집어 9로 만드는것은 잘못된 data augmentation이다.

Noise Robustness

noise-robustness

Noise Robustness는 입력데이터에 Noise를 집어넣는것이다. Data Augmentation과 다른점은, 단순히 입력에만 Noise를 집어넣는 것이 아니라 weight에도 집어넣는 것을 의미한다.

정확한 원리가 규명되지는 않았고, 실험결과 상 데이터 풀이 많아질 뿐 아니라, weight 값을 흔들어 모델의 성능에 도움이 된다고 밝혀졌다.

Label Smoothing

Data Augmentation과 비슷하지만, Label Smoothing은 랜덤한 학습 데이터를 두 개 뽑아서 조작하여 사용한다는 차이점이 있다.

Mix-up
- 두 데이터를 섞어서(blending) 사용한다.
- ex - 강아지와 고양이 그림을 겹쳐서 섞음
CutMix
- 두 데이터를 섞는것이 아니라 파트별로 잘라붙인 하나의 데이터를 만든다.
- ex - 강아지 사진의 머리부분과 고양이 사진의 몸부분을 잘라 붙인 사진을 만든다.