CNN의 원리
BoostCamp AI Tech
CNN
Convolution Neural Network
Kernel
Filter
02/03/2021
본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.
CNN
기존의 다층신경망(MLP)는 각 뉴런들이 선형모델과 활성함수로 모두 연결된(fully connected) 구조였다.
이런 다층신경망의 경우는 각 성분 에 대응하는 가중치 행 가 필요했다.
Convolution 연산 이해하기
Convolution 연산은 기존의 MLP 방식과는 달리, 커널(kernel, 필터)을 입력벡터 상에서 움직여가면서 선형 모델과 합성함수가 적용되는 구조이다.
- 는 번째 히든레이어를 의미한다.
- 는 커널(필터) 사이즈를 의미한다.
- 는 가중치 행렬, 즉 커널을 의미한다. 는 모든 에 대해서 같다.
- 이것이 기존 방식과의 가장 큰 차이점이다.
수학적 의미
Convolution 연산의 수학적 의미는 커널을 이용해 신호(signal)을 국소적으로 증폭 혹은 감소시켜 정보를 추출 또는 필터링 하는 것이다. 엄밀히 말하면 CNN에서 사용하는 연산은 convolution이 아니고 cross-correlation이라고 부르지만, 관습적으로 Convolution으로 부르곤 한다.
- 또는 가 들어간 함수값은 신호를 의미한다.
- 또는 만 들어간 함수 값은 커널을 의미한다.
연속변수이든 이산변수이든, 합과 적분의 차이를 제외하고는 연산이 거의 동일하다.
CNN을 수식만으로 이해하기는 어려우므로, graphical하게 이해해보자.
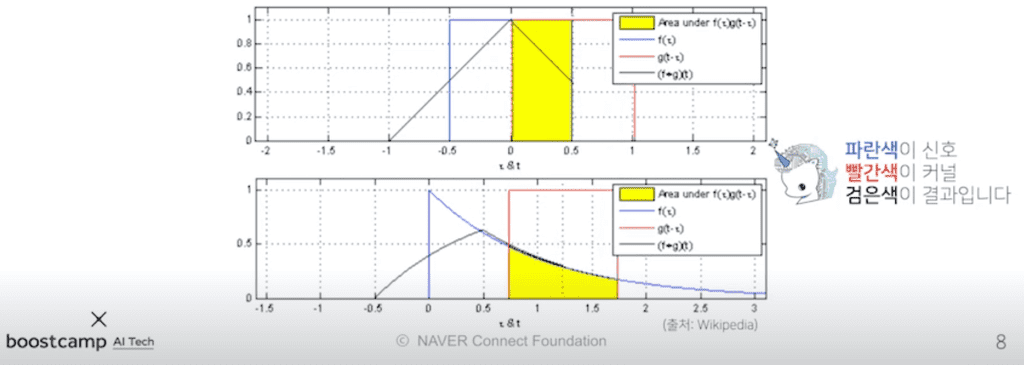
커널은 정의역 내에서 움직여도 변하지 않고(translation invariant), 주어진 신호에 국소적(local)으로 적용된다. 이를 locality가 있다고 말한다.
영상처리
영상처리 강좌 3 - 컨볼루션(Convolution)과 스무딩(Smoothing), 샤프닝(Sharpening)
위 링크에서와 같이, Convolution Network의 커널을 적용할 때 어느 위치를 찍느냐에 따라 하나의 이미지를 여러 형태(blur, emboss, outline 등)로 해석할 수 있다.
다차원에서의 Convolution 연산
데이터의 성격에 따라 사용하는 커널을 다르게 하며, 다차원으로 Convolution 연산을 할 수 있다.
- 여기서는 커널, 는 입력을 뜻한다.
- 데이터의 종류
- 1차원 데이터 - 음성, 텍스트 등
- 2차원 데이터 - 흑백 영상 등
- 3차원 데이터 - 컬러 영상 등
다만, 중요한 것은 위치가 바뀌더라도 커널 의 값은 바뀌지 않는다는 점이다.
2차원 Convolution 연산 이해하기
2차원에서는 1차원과 달리 입력데이터의 형태가 행렬형태이다. 따라서 1차원에서처럼 한쪽 방향으로 한칸씩 움직이면서 커널을 이동시켰던것과 달리, 커널을 x축과 y축 방향으로 한칸씩 움직여가며 적용시킨다.
입력 크기를 , 커널 크기를 , 출력 크기를 라 하면, 출력 크기는 다음과 같이 계산한다.
가령, 28x28 입력을 3x3 커널로 2차원 Convolution 연산을 하면 26x26이 된다.
그러나 실제로 이미지 분석을 하는 경우에는, 2차원이지만 채널이 여러개라 마치 3차원 같은 입력데이터(ex-RGB)가 들어오게 된다. 이런 경우는 2차원 Convolution을 만들어 적용하는데, 입력값의 채널 개수만큼 커널 채널을 만들어주는 것이 포인트이다. 즉, 입력값의 채널 개수와 커널의 채널 개수가 같아야한다.
입력 채널 개수와 커널 채널 개수를 같게하여 합성곱연산을 수행하면, 각 채널의 연산들이 모두 더해지기 때문에 채널이 1이 되어 출력 값의 크기는 (이 된다.
만약 출력 채널의 개수를 여러개로 만들고 싶다면 어떻게 하면 될까? 커널 텐서 자체의 개수를 여러개로 하면된다.
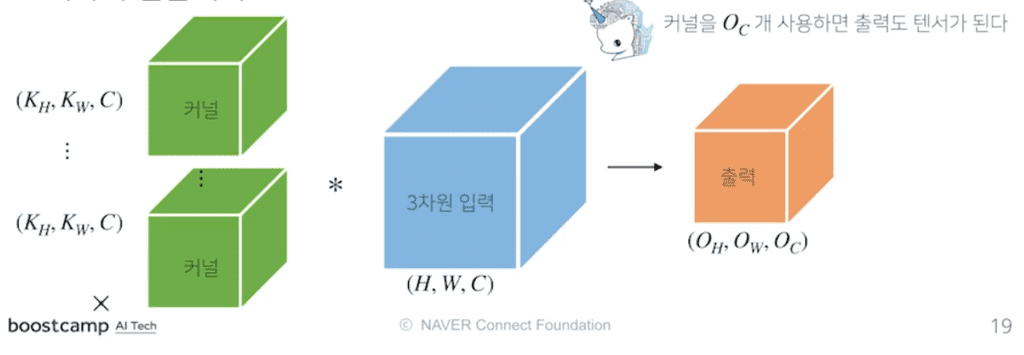
위와 같이 3차원 커널의 개수를 개 사용하면, 출력도 3차원 텐서로 얻을 수 있다. 이것이 오늘날의 CNN 연산에서 사용하는 Convolution 연산의 기본적인 형태이다.
Convolution 연산의 역전파 이해하기
Convolution 연산도 선형변환인 것은 마찬가지이다. 따라서 기존의 역전파 방식과 동일한 방식으로 진행한다.
다만, Convolution 연산은 커널이 모든 입력 데이터에 공통으로 적용되므로, 역전파를 계산할 때(Convolution 연산에 미분할 때)에도 Convolution 연산이 나오게 된다.
는 시그널 에 적용되어, 에 대한 합성곱연산이 된다.
이를 그림으로 이해해보자.
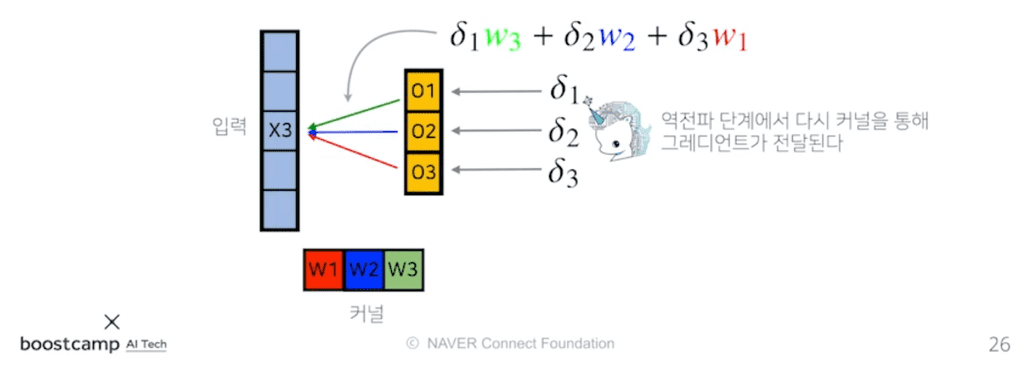
순전파에서, 입력값 는 출력값 으로 갈 때에는 커널의 , 로 갈 때에는 , 로 갈 때에는 파트를 사용했다.반대로, 역전파 과정에서 들어온 미분값 는 순전파 시 적용된 가중치, 즉 커널의 에 곱해져서 Gradient로 전달된다.
이와 같이 역전파 단계에서는, 입력 단계에서 곱해졌던 커널(파트)을 통해 입력값에 Gradient를 전달한다. 그러면 입력값에서 각각의 커널들에는 어떻게 전달될까?
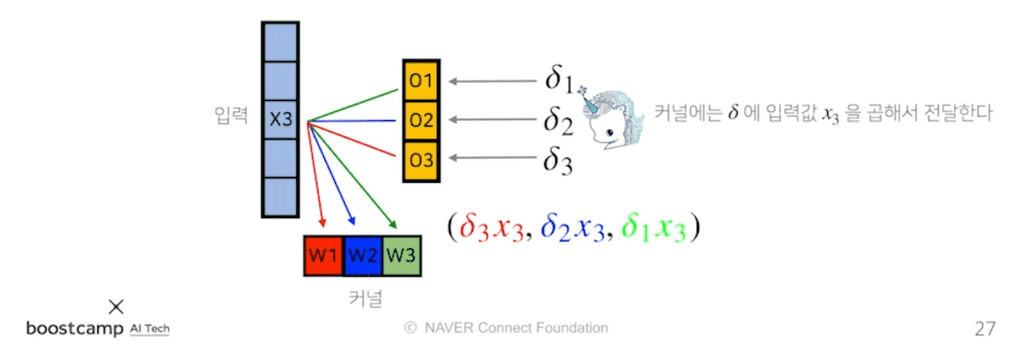
에서 로 전달된 값은, 기존에 적용되었던 커널 으로 다시 전달되므로 커널 은 으로 업데이트된다. 마찬가지로 와 도 각각 으로 업데이트된다.
그런데, 각각의 커널들은 뿐만 아니라 다른 입력값에 대해서도 동일하게 적용되었으므로, 각 커널로 들어오는 Gradient를 모두 합해줘야한다.
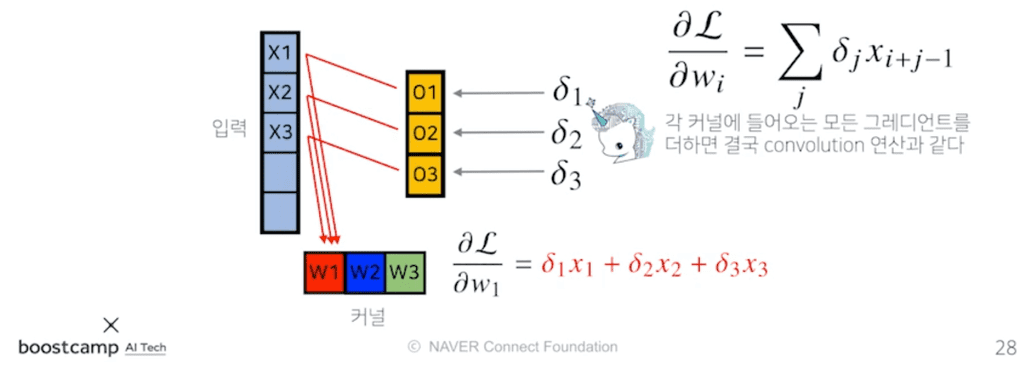
이렇게 각 커널로 들어오는 모든 gradient들을 다 더하면 결국 convolution 연산과 동일한 연산이 이루어진다.
