RNN의 원리

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

Recurrent Neural Network

Recurrent Neural Network(RNN, 순환신경망)는 이전까지 다뤘던 CNN 등과는 달리, 시계열 데이터(Time-Series Data) 또는 시퀀스 데이터(Sequence Data)를 다루는 데에 주로 사용되는 모델이다.

시퀀스 데이터

시퀀스 데이터란

시퀀스 데이터란 순차적으로 들어오는 데이터를 일컫는다. 소리, 문자열, 주가 등이 있다.

시퀀스 데이터에서는 정보들이 시간 순서대로 종합되어서 시점별로 나타난다. 따라서 이벤트의 발생 순서가 데이터의 중요한 요소로서 동작한다.

기존의 데이터에 비해 시퀀스 데이터에서 유의할 점은, 독립동등분포(independant identically distributed, i.i.d)를 위배하기 쉽다는 것이다. 맥락과 순서가 중요하기 때문에, 순서를 바꾸거나 과거 정보에 손실이 발생하면, 데이터의 확률 분포가 바뀌거나 미래 예측의 정확도가 떨어지게 된다.

시퀀스 데이터를 다루는 방법

이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위하여, 조건부확률을 이용할 수 있다.

현재 시점인 $t$ 까지의 확률분포를 알기 위해, $t-1$까지의 확률분포를 구한다. $t-1$의 확률분포를 구하기 위해 $t-2$까지의 확률분포를 구한다. 이를 반복하여 최초까지 내려가면, 최초의 시점부터 순차적으로 조건부확률을 곱하는 식으로 일반화할 수 있다.

다만, 위의 조건부확률과는 달리 시퀀스 데이터를 분석할 때 일반적으로는 과거의 모든 정보(즉, 최초시점부터의 모든 정보)를 사용하지는 않는다. 최근 어느 시점까지의 정보를 이용하거나, 몇 개의 과거 정보들을 truncation하기도 한다. 필요성에 따라서 어느 시점까지 데이터를 활용할 지 모델링이 달라질 수 있다.

따라서, $X_{t+1}$을 예측하기 위한 조건부확률에 들어가는 데이터 길이 $X_{t},X_{t-1},\dots,X_1$는 가변적이므로, 시퀀스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요하다.

가변적인 길이나 아니라 고정된 길이 $\tau$만큼의 시퀀스만 사용하는 경우 AR 모델, 즉 자기회귀모델(Autoregressive Model)이라고 부른다. 다만, $\tau$의 길이는 직접 정해주어야하는 하이퍼파라미터가 되므로, $\tau$를 결정할 때에는 어느정도의 설계자의 사전지식이 필요하게 된다.

또, 문제에 따라 먼 과거의 정보들을 고려해야 하기도하고, $\tau$가 바뀌는 경우가 있다. 이런 경우 사용되는 방법이 RNN의 기본 모형인 잠재 AR 모델(Latent Autoregressive Models), 즉 잠재자기회귀모델이다.

이 경우 $X_t$ 를 예측하기 위해 직전정보인 $t-1$ 시점의 정보 $X_{t-1}$를 제외한 나머지 $X_{t-2},\dots$의 정보들을 $H_t$라는 잠재변수로 인코딩하여 이용한다.

따라서, 직전 시점의 정보와 잠재변수$H$ 두 가지만 가지고 예측할 수 있기 때문에 고정된 길이의 데이터를 가지고 모델링 할 수 있게 된다.

이 때 잠재변수 $H_t$를 신경망을 통해 반복 사용하여 시퀀스 데이터의 패턴을 학습하는 모델을 RNN이라고 한다.

RNN 이해하기

RNN의 순전파

가장 기본적인 RNN 모형은 MLP와 유사한 모형이다.

이 때, $W^{(1)}$과 $W^{(2)}$는 시퀀스와 상관없이 불변인 가중치 행렬이다.

이 모델의 문제점은, 입력이 현재 시점($t$)과 관련된 것만 들어오기 때문에, 예측할 때 과거 정보를 다룰 수 없다는 것이다. 따라서 과거 정보를 다루기 위해 RNN에서는 과거의 잠재변수 $H_t$를 복제하여 다음 순서의 잠재변수를 인코딩하는 데에 사용한다.

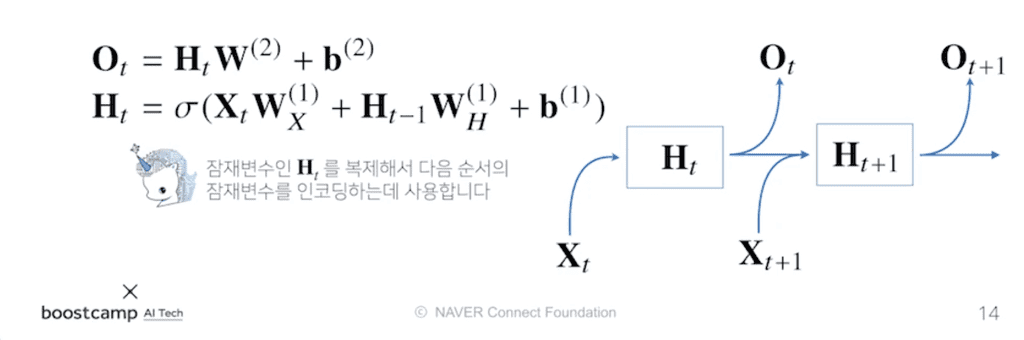
유의할 점은, 가중치 행렬 $W$가 세 개 나온다는 것이다.

• $W_X^{(1)}$ : 입력 데이터에서 선형 모델을 통해 잠재변수로 인코딩하는 가중치 행렬
• $W_H^{(1)}$ : 이전 시점으로 잠재변수로부터 정보를 받아서 현재시점의 잠재변수로 인코딩하는 가중치 행렬
• $W^{(2)}$ : 만든 잠재변수를 출력값으로 만들어주는 가중치 행렬

RNN의 역전파

RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다. 이를 Backpropagation Through Time(BPTT)이라고 한다.

RNN의 모든 시점에서의 예측이 전부 이루어진 다음, 마지막 시점의 Gradient가 타고 올라와서 과거까지 흐른다. RNN은 모든 시간 스텝에서 파라미터 $W$를 공유하므로, 한 시점에서 오류가 역전파되면 이것이 모든 이전시점으로 시간을 거슬러 퍼지게 된다. 그래서 BPTT라는 이름이 붙었다.

위의 그림에서 빨간 선이 역전파과정인데, $H_t$의 역전파에 들어오는 Gradient는 $H_{t+1}$과 $O_t$에서 각각 하나씩 총 두개가 있다.

BPTT 이해하기

BPTT를 통해 RNN의 가중치행렬 미분을 계산해보면, 아래와 같은 미분의 곱으로 이루어진 항이 계산된다.

최종적으로 나오게 되는 Product Term(빨간색 박스가 나타내는 항)은 $i+1$부터 $t$ 시점까지의 모든 잠재변수에 대한 미분값이 곱해지는데, 이 때 시퀀스의 길이(즉, 시점간의 거리)가 길어질수록 해당 항이 불안정해지기 쉬워진다.

• 매 시점마다 1보다 큰 수가 곱해진다면 미분값이 아주 커진다.
• 매 시점마다 1보다 작은 수가 곱해진다면 미분값이 아주 작아진다.

가장 주의해야 하는 것은 작은 수의 미분값이 곱해져 Gradient가 0으로 소실되는 현상(Vanishing Gradient)이다. 이 경우 과거시점으로 갈 수록 Gradient가 점점 작아지기 때문에 과거 시점의 정보가 제대로 반영이 되지 않아 유실된다. 이러면 긴 시퀀스를 분석해야하거나 문맥적인 부분이 중요한 모델의 경우 좋은 결과를 얻을 수 없다.

따라서 시퀀스 길이가 너무 길어지는 경우 길이를 끊는 것이 필요한데, 이를 truncated BPTT라고 부른다. 과거의 일정 시점마다 블럭을 나눠서 해당 블럭 단위로만 backpropagation 연산을 하는 방법이다.

그러나 이 방법이 완전히 기울기 소실 문제를 해결하지 못하므로, 일반적으로는 Vanilla RNN을 사용하지 않고 좀 더 발전한 RNN( LSTM, GRU)을 사용한다.