NLP 06 - Beam Search와 BLEU 평가법

BoostCamp AI Tech

NLP

Natural Language Processing

Beam

BLEU

02/17/2021

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

Beam Search

한계 인식

Seq2Seq의 문제점

기존의 seq2seq 모델은 매 time step마다 가장 높은 확률을 가지는 단 하나의 다음 단어를 예측하는 task를 학습한다. 이를 Greedy Decoding이라고 한다.

그러나 이 방식은 시퀀스로서의 문장 전체를 보고 예측하는 것이 아니라, 근시안적으로 현재 time step에서 가장 좋아보이는 값을 예측하므로, 잘못 예측한 단어를 한번 내놓으면 되돌릴 수 없다.

Exhaustive search

번역의 형태를 수식으로 표현하면 다음과 같다.

\begin{aligned} P(y|x) &= \textcolor{orange}{P(y_1|x)}\textcolor{purple}{P(y_2|y_1,x)P(y_3|y_2,y_1,x)\dots P(y_T|y_1,\dots,y_{T-1},x)} \\ &= \prod^t_1P(y_t|y_1,\dots,y_{t-1},x) \end{aligned}

입력 시퀀스 $x$ 가 주어졌을 때, 가장 그럴듯한 출력 시퀀스 $y$ 를 얻기 위해서는 joint probability, 즉 우변의 모든 항들이 다 곱해졌을 때( $\prod^t_1P(y_t|y_1,\dots,y_{t-1},x)$ ) 가장 큰 값이 나와야 한다.

그러나, 기존의 Seq2Seq 값은 첫번째 단어인 $y_1$ 의 확률 $\textcolor{orange}{P(y_1|x)}$ 를 구할 때, 뒤의 확률들을 고려할 여력이 없기 때문에, 단순히 $\textcolor{orange}{P(y_1|x)}$ 을 최대화시키는 greedy한 방식을 취하게 된다.

그러나 전체적인 관점에서 만약 $\textcolor{orange}{P(y_1|x)}$ 가 지금 당장은 작더라도, $\textcolor{purple}{P(y_2|y_1,x)P(y_3|y_2,y_1,x)\dots P(y_T|y_1,\dots,y_{T-1},x)}$ 가 더 커져서 결과적으로 최대의 확률을 얻을 수 있게 만드는 것이 이상적인 방법일 것이다.

이 방법을 어떻게 구현할 수 있을까? 직접 모든 가능한 시퀀스 $y$ 를 계산해볼까? (Exhaustive Search - Brute Force 방식)

이는 매 step $t$ 마다 vocabulary 크기인 $V^t$ 의 가짓수만큼(즉, $V_n^t$ 를 선택했을때의 확률들) 모두 고려해야한다는 말이다. $O(V^t)$ 는 당연히 기하급수적으로 증가하므로 현실적으로 불가능하다.

이에 대해 차선책으로 나온 방식이 Beam Search이다.

Beam Search

Beam Search란?

매 step $t$ 마다 하나의 단어만을 고려하는 Greedy와, 매 step $t$ 마다 모든 단어를 고려하는 Exhaustive의 절충안으로, Beam Search 는 정해놓은 $\textcolor{red}{k}$ 개만의 단어를 고려한다. 이 $k$ 개의 경우에 해당하는 decoding output을 hypothesis 라고 부른다.

$k$ 는 beam size라고 부르며, 일반적으로 약 5~10개이다.

최대화하고자 하는 beam 값, 즉 hypothesis는 joint probability인데, 이 값에 log를 취하게 되면 각각의 확률들을 덧셈으로 표현할 수 있게 된다.

$score(y_1,\dots,y_t)= logP_{LM}(y_1,\dots,y_t|x) = \sum^t_{i=1}logP_{LM}(y_i|y_1,\dots,y_{i-1},x)$

$\log$ 함수는 원래 단조증가하는 형태이기 때문에, $\log(x)$ 의 $x$ 가 커지면 커질수록 더 큰 값을 가지게 된다. 따라서, 로그함수를 취한 값으로도 동일하게 hypothesis를 최대화할 수 있다.

이와 같은 방식으로 Beam Search는 globally optimal solution, 전역 최적해를 가져다 주지는 않지만, exhaustive search보다는 훨씬 나은 효율을 보여준다.

동작 예시

아래의 예시는 $k$ 가 2인 예시이다.

beam-search1

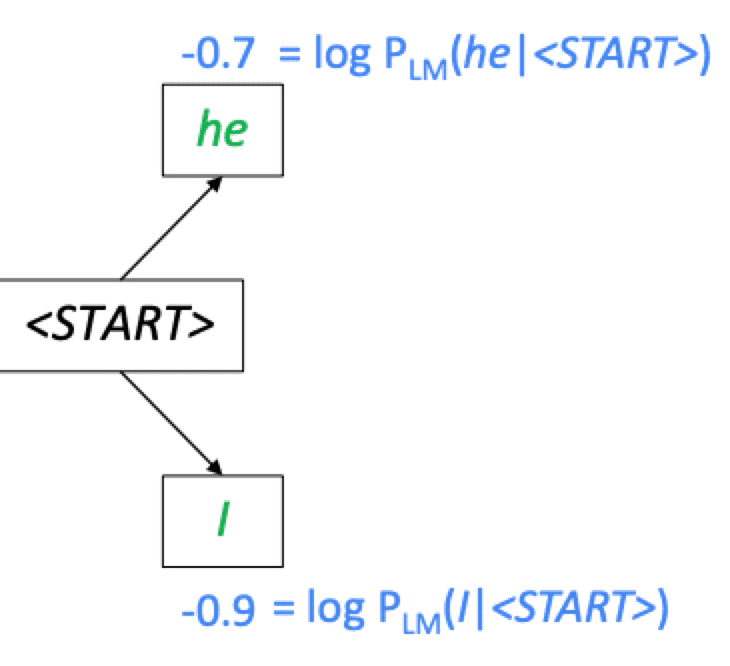
여기서 log를 취한 값이 음수가 나옴을 알 수 있는데, log 함수의 입력값이 0과 1사이의 범위를 가지는 확률값이기 때문이다. 음수이더라도, log 함수는 단조증가 형태이므로 더 높은 확률값을 가지면 더 높은 score로 연결됨을 알 수 있다.

i.e. ['he'의 확률값 > 'I'의 확률값] → [-0.7 > -0.9]

beam-search2

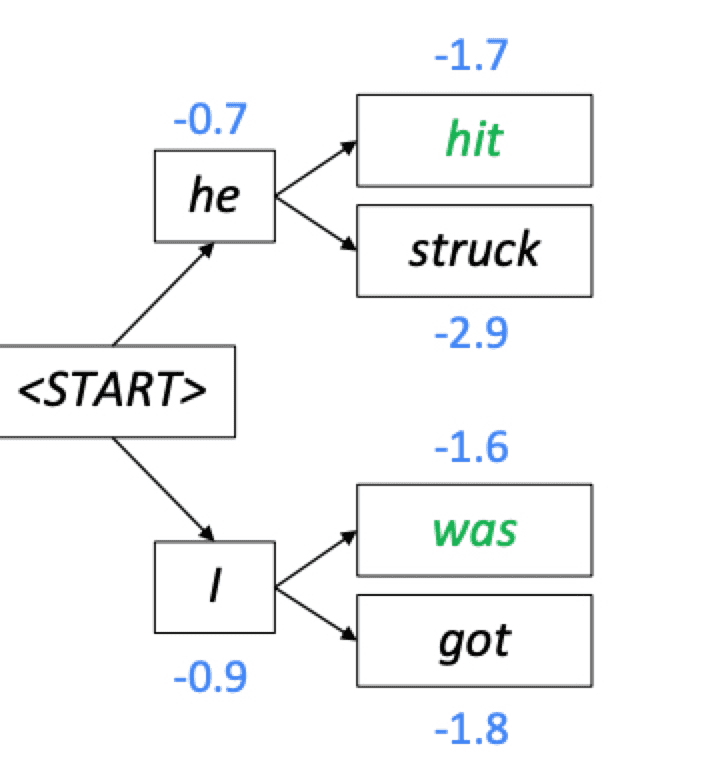
이렇게 매번 score가 가장 높은 $k$ 개만을 골라 다음 search를 진행하므로, 고려해야할 경우의 수가 너무 크게 늘어나지 않는다.

beam-search3

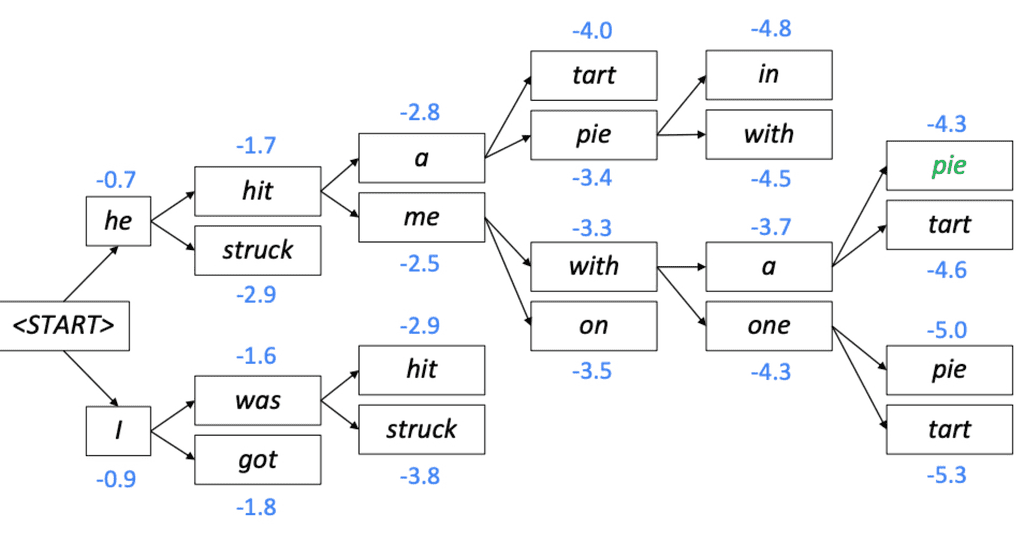
이 과정이 마무리 되면, 나온 모든 값들 중 최종 score가 높은 하나의 시나리오를 뽑고, 해당 시나리오를 output으로 하는 decoding을 출력하게 된다.

Stopping Criterion

Beam Search 디코딩에서, 여러 hyptothesis(시나리오)들은 서로 다른 time step에서 <END>토큰을 생성하게 된다. 즉, 끝나는 시기가 각각 다르다.

<END> 토큰을 생성한 hypothesis는 완료 상태가 되어 따로 저장된다. 이후 모든 hypothesis가 끝나면 score를 비교한다.

Finishing up

최종 score는 결국 다음과 같이 도출된다.

score(y_1,\dots,y_t) = \log P_{LM}(y_1,\dots,y_t|x) = \sum^t_{i=1}\log P_LM(y_i|y_1,\dots,y_{i-1},x)

그런데 score는 joint probability에 log함수를 취하여 음수들의 덧셈연산으로 바꾼 것인데, 확률값은 0과 1 사이이므로 log 함수값들을 합치면 점점 음수가 더해진다. 따라서 길이가 길 수록 더 많은 j, 긴 hyphothesis가 더 낮은 score를 가지는 문제가 생긴다.

따라서 이를 해결하기 위하여 각 hyphotesis를 가지고있는 단어의 개수(즉, 길이)로 나누어 score를 normalize 시켜줄 수 있다.(Normalize by length)

score(y_1,\dots,y_t) = \textcolor{red}{\frac{1}{t}}\sum^t_{i=1}\log P_{LM}(y_i|y_1,\dots,y_{i-1},x)

BLEU

BLEU는 자연어 생성모델에서 모델의 품질(결과의 정확도)를 평가하는 방식이다.

기존의 Seq2Seq with attention 등의 모델을 통해 자연어 생성 task를 수행하여 문장을 만들었을 때, target 문장과 비교하여 정확도를 측정할 수 있다.

그런데 만약 time step별로 정답 문장과 예측 문장의 단어들을 비교하면, 중간에 한 단어를 빼먹거나 한 단어를 추가로 잘못 생성하기만 했어도 한칸씩 밀려서 정확도가 굉장히 낮아지게 된다. 이는 문장 전체를 비교하고 유사도를 평가하는 것이 아니므로 잘못된 방식이 될 것이다.

따라서 정확도를 측정하기 위해서는, 생성한 sequence 문장과 ground truth 문장 사이의 전체적인 유사도를 평가할 필요가 있다. 이를 위한 방식으로, precision과 recall 방식을 생각 해 볼 수 있다.

Precision과 Recall

precision(정밀도) : 예측값 중에 얼마나 정답이 많은가? - 예측의 정확도

recall(재현율) : 정답의 정보들을 얼마나 빠짐없이 재현했는가? - 정답의 재현도

예를 들어, 다음과 같은 두 문장을 생각해보자.

Reference(정답) : She put my name with yellow hearts

Predicted(예측) : She took my name and gave yellow letters

precision = \frac{\#(correct\_words)}{length\_of\_prediction} = \frac{4}{8} = 50\%\\ recall = \frac{\#(correct\_words)}{length\_of\_reference} = \frac{4}{7} = 57\%

모델의 품질을 평가하기 위해 precision과 recall이라는 각기 다른 두 값을 평균내서 나타낼수도 있을 것이다.

이 때, 평균의 종류는 3가지가 있는데, 다음과 같다.

\begin{aligned} 산술평균 &= \frac{a+b}{2} \\ 기하평균 &= \sqrt[2]{a+b} \\ 조화평균 &= \frac{1}{\frac{\frac{1}{a}+\frac{1}{b}}{2}}\\ \end{aligned}\\ 산술평균\geq 기하평균 \geq 조화평균

내분점의 관점에서 보자면, 조화평균과 기하평균은 작은 값에 더 가중치를 많이 두는 방식이다.

1:1 내분점(산술평균)보다 작은 쪽에 치우쳐져 있기 때문이다.

F-measure

F-measure = \frac{precision\times recall}{\frac{1}{2}(precision+recall)} = \frac{0.5\times0.57}{0.5\times(0.5+0.57)} = 0.53

F-measure는 precision과 recall을 이용할 때 조화평균을 이용하는 방식으로, 좀 더 작은 쪽에 가중치를 두어서 평가하는 방식이 된다.

그러나 위에서 제시한 품질평가방법들은 순서를 고려하지 않으므로, 정답 단어들이 뒤죽박죽 섞여있더라도 정확하다고 평가하는 오류를 가진다.

이를 해결하기 위해 BLEU 스코어가 나왔다.

BLUE score

BLUE score란?

BiLingual Evaluation Understudy(BLEU)는 기존의 정확도 평가 방식에 추가적으로 순서까지 고려한 평가방식이다.

BLEU = \underbrace{min(1,\frac{length\_of\_prediction}{length\_of\_reference})}_{\text{brevity penalty}}\underbrace{(\prod^n_{i=1}precision_i)^{\frac{1}{n}}}_{\text{n-gram}}

'정답 문장의 단어들과 겹치는 개별 단어가 얼마나 있는가'를 반영하면서도, 추가적으로 'n개의 연속된 단어(n-gram)가 얼마나 정답 문장의 단어연속체와 겹치는가'를 평가에 반영한다.

이 때 n은 일반적으로 1-4개 정도이다.
precision만 반영하고, recall은 관여되지 않는다.
- 예시 : The horse is very fast.
- 위의 문장에서 very가 빠진다고 해서 번역의 질이 크게 떨어지지 않는다.
- 다만, 어떤 단어(horse)를 아예 다른 단어(morse)로 나타냈을 경우 문장의 의미가 달라져버리는 경우가 생기기 때문에 precision은 고려한다.
precision의 곱들을 기하평균 취한다.
- 산술평균에 비해 작은 쪽에 좀 더 가중치를 주기 위해서이다.
- 조화평균을 쓰지 않은것은 작은 쪽에 지나치게 큰 가중치를 주기 때문이다.

brevity penalty는 정답 문장에 비해 너무 적은 문장을 생성했을 경우 더 작은 값을 곱해주어 페널티를 주는것이다.

예측 문장의 길이가 정답 문장의 길이보다 짧으면, 1보다 작은 수를 곱하므로 정확도가 낮아진다.
반대로 생각해보면, 정답문장의 모든 단어들이 존재하면 예측문장에 존재하면, 예측 문장의 길이가 정답 문장의 길이보다 길더라도, 최대 1밖에 곱해지지 않는다. 그런 점에서 recall의 최댓값으로 1이 나오는것과 동일하게 볼 수 있으므로, recall을 어느정도 고려한 모델이 된다.

Reference

NMT - cs234n

WRITTEN BY

욕심많은 알파카

알파카의 Always Awake Devlog

Seoul

Email GitHub Facebook Instagram