경사하강법(Gradient Descent)의 기초와 이해
BoostCamp AI Tech
numpy
Grdient Descent
01/26/2021
본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 수강한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.
경사하강법
미분(differentiation)
미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로, 최적화에서 가장 많이 사용되는 기법이다.
Python은 sympy.diff를 이용해 미분을 계산할 수 있다.
import sympy as symfrom sympy.abc import xsym.diff(sym.poly(3*(x**2) + 5*x + 1), x) # 다항함수를 x로 미분하라# Poly(6𝑥+5,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ)미분의 의미
미분은 함수 의 주어진 점 에서의 접선의 기울기를 구하는 과정이다.
한 점에서 접선의 기울기를 알면, 어느 방향으로 움직여야 함수값이 증가 / 감소하는지 알 수 있다.
2차원에서의 그래프를 보면 쉽게 어느 방향으로 움직여야 할 지 알 수 있지만, 10차원, n차원 등의 고차원에서는 이를 추측하기 어렵다. 따라서 미분값을 이용해 값의 변경 방향을 알 수 있다.
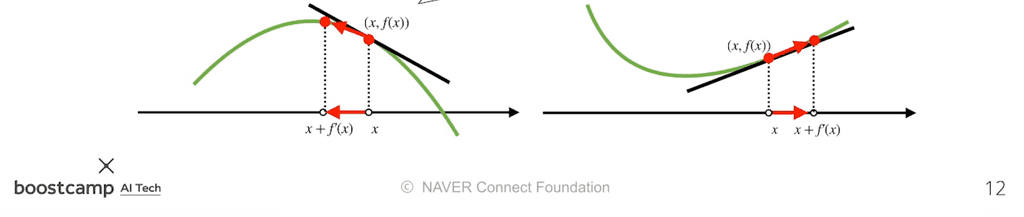
- 이 때, 함수 값을 증가시키고 싶다면 미분값을 더하고, 감소시키고 싶으면 미분 값을 뺀다.
- 미분값이
양수이면, 증가하는 기울기에 있으므로미분값을 더했을 때, 오른쪽으로 이동하여함수값이 증가하게 된다. - 미분값이
음수이면, 감소하는 기울기에 있으므로미분값을 더했을 때, 왼쪽으로 이동하여함수값이 증가하게 된다. - 미분값이
양수이면, 증가하는 기울기에 있으므로미분값을 뺐을 때, 왼쪽으로 이동하여함수값이 감소하게 된다. - 미분값이
음수이면, 감소하는 기울기에 있으므로미분값을 뺐을 때, 오른쪽으로 이동하여함수값이 감소하게 된다.
- 미분값이
미분을 어디에 사용할까? - 경사법
이와 같이,
- 미분값을 더하는 것을
경사상승법(gradient ascent)라고 하며 함수의 극대값 위치를 구할 때 사용한다. - 미분값을 빼는 것을
경사하강법(gradient descent)라고 하며, 함수의 극소값 위치를 구할 때 사용한다.Full Batch Gradient Descent이라고도 부른다.
경사상승법/경사하강법은 극값에 도달하면 미분값이 0이므로 더이상 업데이트가 되지 않아 움직임을 멈춘다.- AI에서는, 목적함수 최적화가 자동으로 끝났음을 의미한다.
'''Input: gradient, init, lr, epsOutput: var'''# gradient : 미분을 계산하는 함수# init : 시작점, lr : 학습률, eps : 알고리즘 종료 조건var = initgrad = gradient(var)# 컴퓨터로 계산할 때 미분이 정확히 0이되는 것은 불가능하다.# 따라서, 충분히 작을 때(eps보다 작을때) 종료하는 조건이 필요하다.while(abs(grad) > eps): # lr은 학습률로, 미분을 통해 업데이트하는 '속도'를 조절한다. var = var - lr * grad # 종료조건이 성립하기 전까지는 미분값을 계속 업데이트한다. grad = gradient(var)Gradient 벡터
변수가 벡터라면
그런데 입력값이 이차원 공간의 점이 아니라, n차원 공간의 점인 벡터라면 어떨까? 그래프를 따라 왼쪽, 오른쪽으로만 이동하는 것이 아니라, n차원이기 때문에 굉장히 많은 방향으로 이동할 수 있을 것이다. 이 경우 단순한 미분으로는 함수값의 변화을 측정하기 힘들다.
이처럼 벡터가 입력값인 다변수 함수의 경우, 편미분(partial differentiation)을 사용한다.
이 때, 는 번째 값만 1이고 나머지는 0인 단위벡터() 를 의미한다.
편미분도 sym.diff 로 계산이 가능하다. x, y등의 변수를 여러 개 사용한 다변수 함수(sim.poly)를 집어넣으면 된다.
import sympy as symfrom sympy.abc import x,ysym.diff(sym.poly(3*(x**2) + 5*x*y + 2*y + 1) + sym.cos(2*x + 2*y), x)# 6𝑥+5𝑦−2sin(2𝑥+2𝑦)각 변수별로 편미분을 계산한 gradient 벡터를 경사하강법/경사상승법에 이용할 수 있다.
위의 식에서 삼각형을 거꾸로 뒤집어놓은 모양의 기호를 nabla 라고하는데, 대신 벡터 를 이용해서 변수 를 동시에 업데이트할 수 있다.
3차원공간 상에 다음과 같이 다변수 함수를 표현한다고 생각해보자.
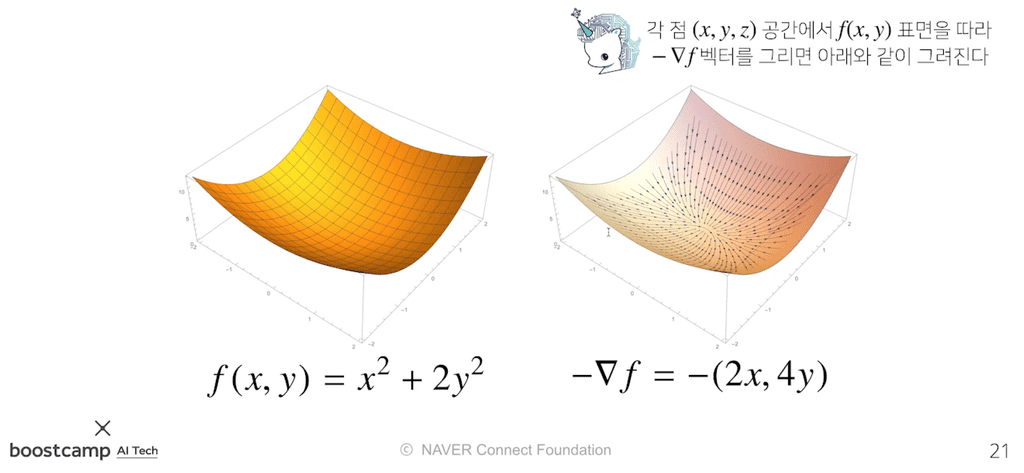
이 때, 이를 등고선으로 옮기면 다음과 같다.
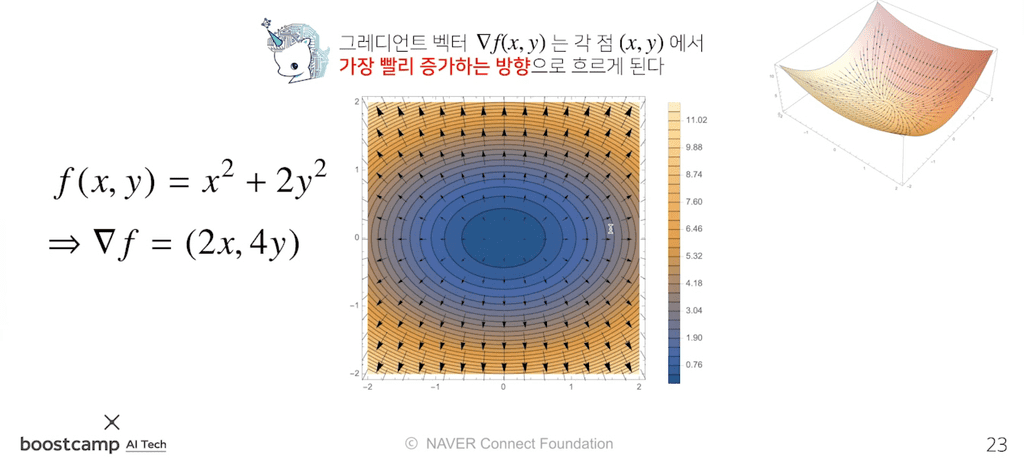
- gradient 벡터 는 각 점 에서 가장 빨리 증가하는 방향과 같다.
- gradient 벡터 는 와 같고, 이는 각 점 에서 가장 빨리 감소하는 방향과 같다.
이는 임의의 차원 에서도 성립한다.
변수가 벡터일때의 경사하강법
변수가 벡터로 바뀌었을 때, 경사하강법의 알고리즘은 종료 조건 하나만 바뀌면 된다.
# 경사하강법 with 벡터'''Input: gradient, init, lr, epsOutput: var'''# gradient : "Gradient 벡터"를 계산하는 함수# init : 시작점, lr : 학습률, eps : 알고리즘 종료 조건var = initgrad = gradient(var)# 절대값(abs) 대신 norm을 계산해서 종료 조건을 설정한다.while(norm(grad) > eps): var = var - lr * grad grad = gradient(var)경사하강법으로 선형회귀 계수 구하기
기존에 무어-펜로즈 역행렬을 이용하여 선형회귀모델을 구했었는데, 이는 경사하강법으로도 구해볼 수 있다.
풀이
선형회귀의 목적식은 이고, 선형회귀의 목적은 이를 최소화하는 를 찾는 것이다.
따라서 목적식을 로 미분한다음, 주어진 에서 미분값을 뺀다면, 경사하강법 알고리즘으로 최소에 해당하는 점을 구할 수 있다.
다음과 같은 Grdient 벡터를 구해보자.
이 때 의 k번째 계수에 해당하는 를 가지고 목적식을 편미분하는 식을 풀어서 보면 아래와 같은 식이 된다.
여기서 조심할 점은, 일반적인 수학의 과 풀이 방식이 살짝 다르다는 것이다.
여기서 사용하는 은 모델 학습에 사용되는 것이므로, n개의 데이터셋을 가지고 있다는 가정하에 출발한다. 따라서 단순히 에 을 바로 씌우는 것이 아니라, 로 평균 내준 뒤에 씌워준다.
이 때에 사용되는 loss는 RMSE(Root Mean Squared Error)이다. 다음과 같은 도출과정을 따른다.
- 벡터의 거리는 으로 계산한다.
SE(Sqaured Error)는 각 데이터별로 정답과 예측 벡터의 차이를 의 제곱으로 계산한다.MSE (Mean Squared Error)는SE를 데이터의 숫자만큼 나누어준다.(평균내기)RMSE (Root Mean Squared Error)는MSE에 제곱근을 취해준다.
사실 정확히 쓰면 기대값 기호를 붙여 라고 써야하지만,
norm의 기호가 원래 확장성이 있기도 하고, 관용적으로 RSME를 처럼 쓴다고 한다.
이를 계산하여 정리하면 다음과 같다.
- 원래 목적식이었던 는 분모로 간다.
- 을 씌우기 전의 식인 와, 행렬 의 번째 열벡터를 전치(시킨 행렬을 곱해준 것이 분자로 가게 된다.
- 이 때, 는 결국 를 계수 에 대해 미분한 결과인 과 같다.
- 이 식은 곧 , 즉 k번째 계수에 대한 편미분과 같다.
이제, 목적식을 최소화하는 를 구하는 경사하강법 알고리즘을 다음과 같이 표현할 수 있다.
- t번째 단계에서의 를 로 정의한다.
경사하강법은 함수값을 최소화시키기 위하여 에서 미분값(을 빼는 것으로 업데이트시켜주는 방식이다.- 여기에서는 기존의 식을 다변수 함수에 적용시키는 것이다.
- 목적식을 최소화시켜야하므로 에서 (편)미분값 를 빼주는 것으로 업데이트한다.
- 이때 편미분 값을 위에서 구했던 식으로 치환하면, (기존의 식이 음수였으므로 부호가 양수로 바뀐) 두번째 식을 얻을 수 있다.
이와 같이 계산하게되면 사실 제곱근을 계산하는 것이 다소 귀찮은 편인데, 어차피 을 최소화하는 것이나 을 최소화하는 것이나 방향은 같다.
따라서 Gradient 벡터 계산의 편의를 위해 가 아닌 를 최소화하기도 한다.
이 경우, 경사하강법 알고리즘도 다음과 같이 비교적 간단해지게 된다.
경사하강법 기반 선형회귀 알고리즘
실제 값과 계산 값의 차이 를 Error Term 이라고 정의하자.
에 에러텀을 곱한 값이 곧 Gradient 벡터가 된다는 것을 앞에서 수식으로 증명했으므로, 이것을 이용해서 를 업데이트하는 경사하강법 알고리즘을 짜보면 다음과 같다.
'''Input: X, y, lr, TOutput: beta'''# norm : L2-노름을 계산하는 함수# lr: 학습률, T: 학습횟수# 기존의 eps처럼 gradient 벡터가 특정 값 이하로 떨어질 때까지 수행할수도 있지만,# 특정 시간동안만 학습하도록 시간을 제한하고 싶다면 횟수 T를 지정해 줄 수도 있다.for t in range(T): # L2-norm의 제곱을 계산해서 beta를 업데이트한다. error = y - X @ beta grad = - transpose(X) @ error beta = beta - lr * grad위와 같은 경사하강법 알고리즘을 이용해, 무어-펜로즈 역행렬을 사용하지 않고도 계수 를 찾을 수 있다.
# numpy를 활용한 경사하강법 수행 예시import numpy as npX = np.array([[1,1],[1,2],[2,2],[2,3]])y = np.dot(X, np.array([1,2])) + 3beta_gd = [10.1, 15.1, -6.5] # [1,2,3]이 정답 - 지금 값은 무작위 값# intercept항 추가# y 절편을 추가하면, y = ax + b의 b가 bias term의 역할을 해서 계산이 용이하다.X_ = np.array([np.append(x,[1]) for x in X])for t in range(5000): error = y - X_ @ beta_gd # error = error / np.linalg.norm(error) grad = - np.transpose(X_) @ error beta_gd = beta_gd - 0.01 * gradprint(beta_gd)# [1.00000367 1.99999949 2.99999516]위의 식에서는 학습률과 학습횟수를 크게 다루지 않았지만, 실제 적용에서는 학습률과 학습 횟수가 중요한 hyperparameter가 된다. 학습률과 학습 횟수에 대해서는 이후 구현과정에서 더 상세하게 다뤄보자.
경사하강법이 수렴하지 않을 때 - 확률적 경사하강법
이론적으로, 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해서는, 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어있다.
특히, 선형회귀의 목적식 는 회귀계수 에 대해 볼록함수이므로, 알고리즘을 충분히 돌렸을 경우 수렴이 보장된다.
그러나, 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로, 수렴이 항상 보장되지는 않는다.
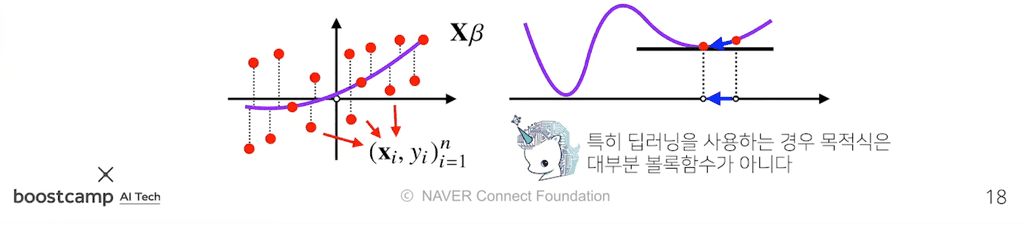
특히 딥러닝을 사용하는 경우는 목적식이 대부분 볼록함수가 아니므로,
이 경우 일반적인 경사하강법이 아닌 확률적 경사하강법(Stochastic Gradient Descent,SGD)을 사용한다.
확률적 경사하강법은 모든 데이터를 사용해서 업데이트 하는 대신에, 데이터 하나 또는 일부를 활용하여 업데이트하는 방식이다.
- 이 때 데이터 하나만 활용하는 경우는 그냥
SGD라고 부른다. - 데이터 일부는
Mini Batch라고 하며, 미니 배치를 사용하는 경우를Mini Batch SGD라고 부른다.- 데이터를 하나만 사용하는것보다 효율이 더 좋다.
- 따라서 오늘날
SGD는 미니 배치를 활용하는 경우가 대부분이며, 이로 인해Mini Batch SGD를 그냥SGD라고 축약해 부르기도 한다.
볼록함수가 아닌(non-convex) 목적식은 SGD를 통해 다음과 같이 최적화할 수 있다.
학습률과 학습횟수를 고려해야하기 때문에 SGD가 만능은 아니지만, 딥러닝의 경우는 SGD가 경사하강법보다 실증적으로 더 낫다고 시간에 걸쳐 검증된 상태이다.
- 일부만 사용하더라도, 모든 데이터를 활용한 Gradient 벡터와 기댓값이 유사하다는 것이 확률적으로 검증되었다.
- 또한, 더 적은 데이터를 가지고 업데이트할 수 있으므로 연산자원을 더 효율적으로 활용할 수 있다.
- 전체 데이터를 쓰지 않고 미니배치 를 사용해 업데이트하므로 연산량이 으로 감소한다.
확률적 경사하강법의 원리 : 미니배치 연산
경사하강법(GD)은 전체 데이터를 이용해서 목적식의 gradient 벡터를 계산한다.
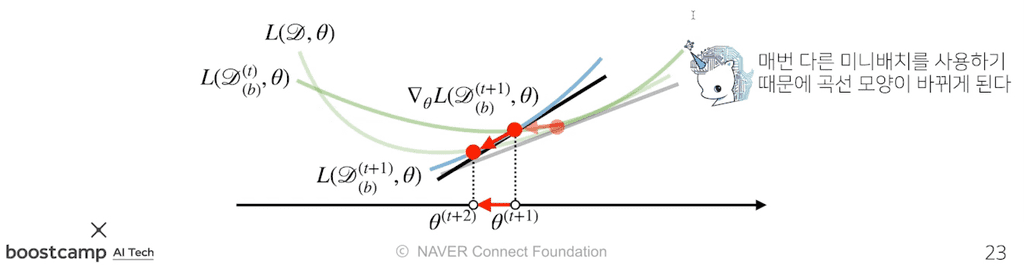
반면, SGD는 미니배치를 가지고 gradient 벡터를 계산한다. 미니배치는 확률적으로 선택된 데이터 묶음이므로 매 step마다 다른 미니배치를 사용할 때마다 목적식의 모양이 점점 바뀌게 된다.
- 그렇지만 방향은 얼추 비슷할 것이다.
- 이렇게 목적식의 모양이 바뀌게 되면서,
경사하강법에서는 미분값이 0이되는 극소점이SGD에서는 극소값이 아니게 된다. - 즉, local minimun(극소점)을 탈출할 수 있다.
- 이 원리로 non-convex 함수에서도 최소점을 찾는 데에 활용할 수 있다.
- 극소점을 탈출할 수 있으므로 global minimum을 탈출할 수도 있다.
- 이는
SGD의 단점 중 하나로, global minimum 근처까지는 빠르게 수렴하지만 정작 정확한 global minimum 극소값에는 도달하지 못하고 진동하는 경우가 많다. - 반면,
GD는 연산량과 시간이 많이 필요하지만 전체 배치를 통해 모든 점에서 일정한 목적식을 사용하여 global minimum으로확실히수렴 가능하다.(convex function인 경우) - 이와 같은
SGD의 문제점은 learning rate를 점점 줄여나가는 방식으로 step size를 줄임으로써 어느정도 해결할 수 있다.
- 이는
- 반대로 말하자면, 일반적인
GD은 매 step 목적식이 바뀌지 않으므로 local minimum 도달시 탈출이 불가능하다.
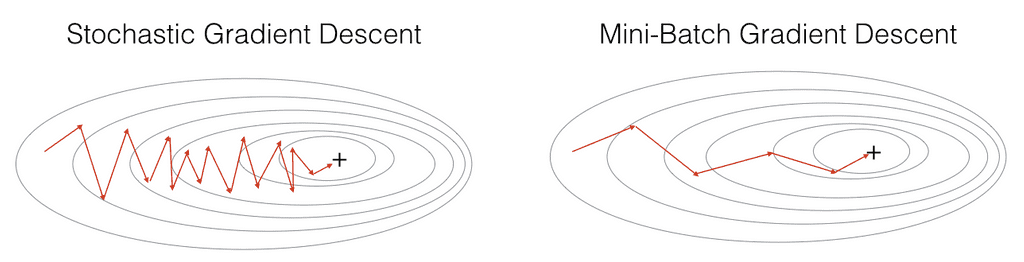
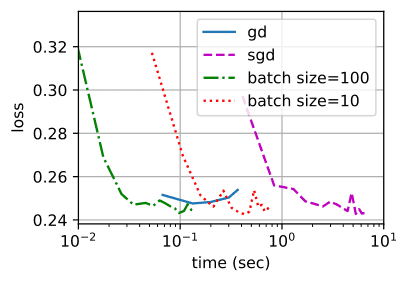
(출처: Dive into Deep Learning)
SGD는 볼록이 아닌 목적식에서도 사용 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적이다.
- 다만, 경사하강법처럼 정확하게 gradient 벡터를 계산해서 흐르는것이 아니므로, 이동방향이 좀 튀는 경향이 있다.
- 그렇지만, 결국 데이터를 가지고 gradient 벡터를 계산해서 움직이기 때문에 최솟점으로 향한다는 것은 같다.
- 또한, 미니배치를 가지고 연산하므로, 각각의 gradient 벡터 계산에 있어서 연산속도가 훨씬 빠르다.
단, SGD에서는 기존의 경사하강법에서 고려했던 학습률(learning rate), 학습횟수(T)에 더해 미니배치 사이즈까지 고려하여 학습해야한다.
확률적 경사하강법의 원리 : 하드웨어
오늘날 딥러닝의 데이터는 굉장히 많고 사이즈도 크기 때문에, 하드웨어상 경사하강법에 한계가 있다. 일반적인 경사하강법을 사용하여 모든 데이터를 업로드하면, Out-of-memory 오류가 뜨는 경우가 생긴다.
따라서 이러한 점에서 SGD는 필수적인 알고리즘으로 사용되고 있다. 미니배치로 쪼갠 데이터를 활용하여 경사하강법을 업데이트할 수 있으므로 좀 더 빠른 연산이 가능하고, 하드웨어의 한계를 극복해 GPU로 병렬연산하는것이 가능해진다.
왜 CPU가 아닌 GPU로 연산하는것이 좋은지 궁금하다면 다음 링크를 참조하자.
CPU와 GPU의 차이
The Continuing Importance of GPUs For More Than Just Pretty Pictures - MCADCafe Editorial
