Graph 05 - 노드 임베딩

본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.

노드 임베딩(정점 임베딩)

정점 표현 학습

정점 표현 학습(Node Representation Learning)은 그래프의 정점들을 벡터 형태로 표현하는 것이다. 간단히 노드 임베딩(Node Embedding)이라고도 부른다.

노드 임베딩은 벡터 형태의 표현 그 자체를 의미하기도 한다. 정점이 표현되는 벡터 공간을 임베딩 공간이라고 하자.

• 정점 표현 학습의 입력은 그래프이다.
• 정점 표현 학습의 출력은 벡터표현 $z_u$로, 각 정점 $u$에 대한 임베딩을 의미한다.($\mathbb{R}_d 차원$)

왜 노드 임베딩을 사용하는가?

노드 임베딩을 하면 그래프의 노드들을 벡터형태로 표현할 수 있게 된다. 즉, 벡터 형태의 데이터들을 위한 도구들을 그래프에도 적용할 수 있다. 그래프를 위한 별도의 알고리즘이 아니라, 기계학습의 방식을 그래프에서 사용할 수 있는 것이다.

• 기계학습 도구들
  • Classifier(로지스틱 회귀분석, MLP 등)
• 최신 ML 기법들을 정점 분류(Node Classificaiton), 군집 분석(Community Detection) 등에 사용할 수 있다.

K-Means, DBSCAN 같은 군집 분석 알고리즘들은 벡터형태로 표현된 사례(instance)들을 입력으로 받는다.

노드임베딩의 목표

노드 임베딩은 그래프에서의 정점간 유사도를 임베딩 공간에서도 보존할 수 있도록 수행되어야한다. 이 때, 유사도로는 내적(Inner Product)를 사용한다.

임베딩 공간에서의 노드 $u$와 노드 $v$의 유사도는 두 노드의 임베딩 출력값의 내적값과 같다. 내적은 두 벡터가 클 수록, 그리고 같은 방향을 향할 수록 큰 값을 갖는다.

인접성 기반 유사도

인접성 기반 유사도(Adjacency-based similarity)에서는 두 정점이 인접할 때 유사하다고 간주한다. 두 정점 $u$와 $v$가 인접하다는 것은 둘을 직접 연결하는 간선 $(u,v)$가 있음을 의미한다.

이를 인접행렬(Adjacency Matrix) $A$로 표현하였을 때, 두 정점 $u$와 $v$ 사이의 간선 $(u,v)$는 $A_{u,v}$로 나타낼 수 있으며, 인접하였을 경우 이 값이 1이고 그렇지 않으면 0이다. 따라서, 인접행렬의 원소 $A_{u,v}$를 두 정점 $u$와 $v$의 유사도로 나타낼 수 있다.

손실 함수

인접성 기반 접근법의 손실 함수(Loss Function)는 다음과 같으며, 손실을 최소화하는 노드 임베딩을 찾기 위해 SGD등이 사용된다.

• $\textcolor{purple}{z_u^{\top}z_v}$ : 임베딩 공간에서의 유사도
• $\textcolor{red}{A_{u,v}}$ : 그래프에서의 유사도
• 임베딩 공간의 유사도와 그래프에서의 유사도 차이가 최소가 되도록 한다.

한계

그러나 인접성 기반의 접근방법은 거리가 1보다 큰 정점들의 유사도를 0으로밖에 계산하지 못하므로, 정점들간의 유사도를 제대로 비교하기에는 무리가 한계가 있다. 또한, 어느 군집에 속했는가(같은 군집인지 아닌지 여부)도 유사도에 반영되지 않는다.

거리/경로/중첩 기반 유사도

거리 기반 유사도

거리 기반 유사도(Distance-based Similarity)에서는 두 정점 사이의 거리가 '충분히' 가까운 경우 유사하다고 간주한다.

• 이 때, '충분히'의 기준은 임의적이다(하이퍼파라미터)

경로 기반 유사도

경로 기반 유사도(Path-based Similarity)에서는 두 정점 사이의 경로가 많을수록 유사하다고 간주한다.

두 정점 $u$와 $v$ 사이의 경로 중 거리가 $k$인 것의 수는 $A_{u,v}^k$, 즉 인접행렬 $A$의 $k$제곱 행렬의 $u$행 $v$열 원소와 같다.

경로 기반 접근법의 손실함수는 다음과 같다.

중첩 기반 유사도

중첩 기반 유사도(Neighborhood-based Similarity)는 두 정점이 많은 이웃을 공유할수록 유사하다고 간주한다. 공유하는 이웃의 수에 비례하여 유사도가 높아진다.

정점 $u$,$v$의 이웃집합을 각각 $N(u)$, $N(v)$이라고 하자. 두 정점의 공통 이웃 수 $S_{u,v}$는 다음과 같이 정의한다.

이 때 손실함수는 다음과 같다.

단순히 공통 이웃 수를 세는 것이 아니라, 자카드 유사도나 Adamic Adar 점수를 사용할 수도 있다.

• 자카드 유사도(Jaccard Similarity) : 공통 이웃의 수 대신 비율을 계산하는 방식

  $$0\le \frac{N(u)\cap N(v)}{N(u)\cup N(v)} \le 1$$

• Adamic Adar 점수 : 공통 이웃 각각에 가중치를 부여하여 가중합을 계산하는 방식. 연결성(Degree)이 높은 노드일수록 가중치가 적다.

  $$\sum_{w\in N(u)\cap N(v)}\frac{1}{d_w}$$

임의보행 기반 유사도

임의보행 기반 유사도(Random walk-based similarity)는 한 정점에서 시작하여 랜덤 워크를 할 때 다른 정점에 도달할 확률을 유사도로 간주한다.

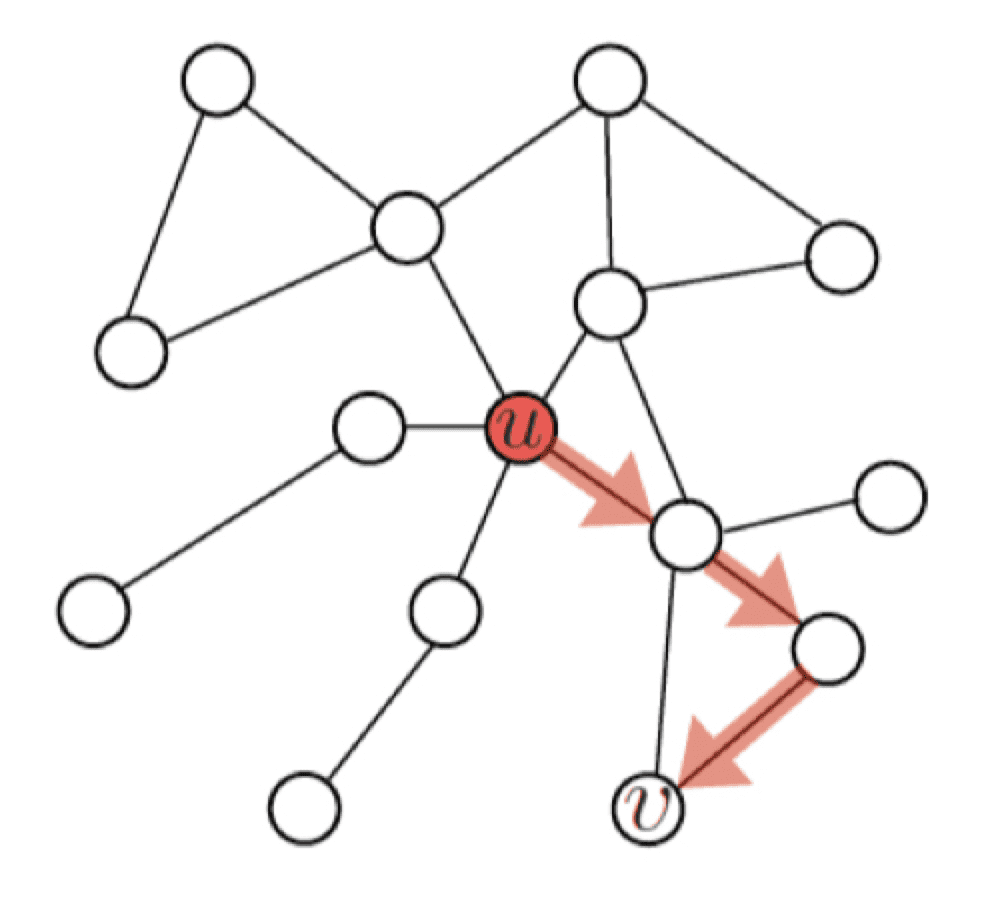
여기서 랜덤워크란, 현재 정점의 이웃 중 하나를 균일한 확률로 선택하여 이동하는 과정을 반복하는 것을 의미한다.

이 경우 시작 정점 주변의 이웃 노드들, 각 노드의 연결성 등에 따라서 확률이 달라진다. 또, 거리기반 유사도처럼 유사도 측정의 최대거리 $k$를 제한하지 않으므로, 그래프의 모든 노드들에 대하여 계산할 수 있게 된다.

따라서, 지역적 정보와 그래프 전역 정보를 모두 고려한다는 장점이 있다.

과정

1. 각 정점에서 시작하여 랜덤 워크를 반복 수행한다.

2. 각 정점에서 시작한 랜덤 워크 중 도달한 정점들의 리스트를 구성한다. 정점 $u$에서 시작하여 랜덤 워크 중 도달한 정점들의 리스트를 $N_R(u)$라고 한다. 한 정점을 여러번 도달한 경우, 해당 정점은 $**N_R(u)$에 여러번 포함될 수 있다**.

3. 다음의 손실함수를 최소화하는 임베딩을 학습한다.

   $$\mathcal{L} = \textcolor{green}{\sum_{u\in V}}\textcolor{orange}{\sum_{v\in N_R(u)}} - \log(\textcolor{blue}{P(v|z_u)})$$

   • $\textcolor{blue}{P(v|z_u)}$ : $u$에서 시작한 랜덤워크가 $v$에 도달할 확률을 임베딩으로부터 추정한 결과를 의미한다. 이 (확률)값이 크면 클수록 좋다.

     $$\textcolor{blue}{P(v|z_u)} = \frac{\exp(z_u^\top z_v)}{\sum_{n\in V}\exp(z_u^\top z_n)}$$
     • 즉, 유사도 $\exp(z_u^\top z_v)$가 높을 수록 도달 확률이 높다.

   • $\textcolor{orange}{\sum_{v\in N_R(u)}}$ : 랜덤 워크 중 실제로 마주친(도달한) 모든 정점에 대하여 합산

   • $\textcolor{green}{\sum_{u\in V}}$ : 모든 시작점마다 수행하여 합산

   DeepWalk와 Node2Vec

   랜덤워크의 방식에 따라 DeepWalk와 Node2Vec으로 나눌 수 있다.

DeepWalk는 위에서 설명했던 것과 같이 균일한 확률의 랜덤워크를 수행한다.

Node2Vec은 2차 치우친 임의보행(Second-order Biased Random Walk)를 사용한다.

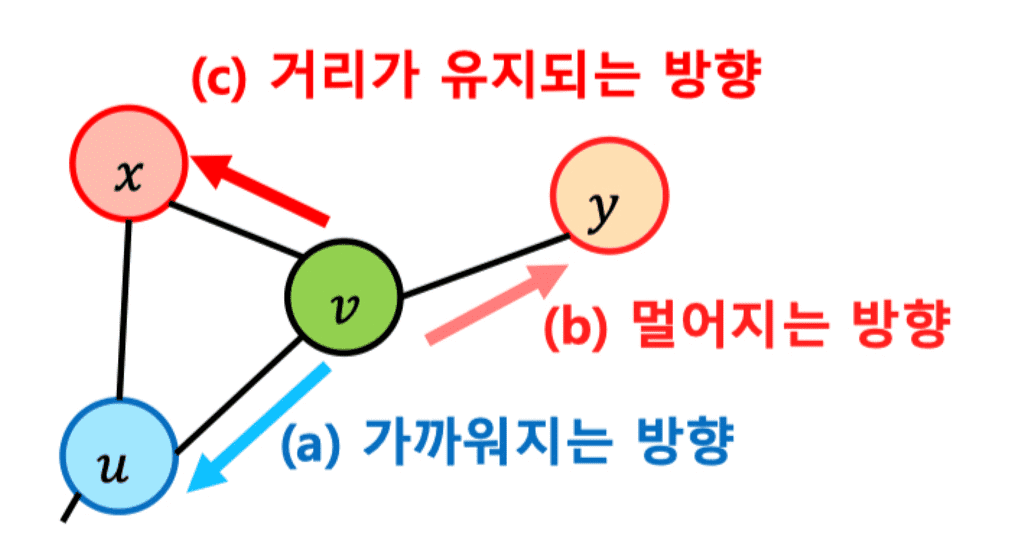
현재 정점($v$)과 직전에 머물렀던 정점($u$)을 모두 고려하여 다음 정점을 선택하며, 직전 정점의 거리를 기준으로 경우(이전의 정점과 거리가 가까워지는/유지되는/멀어지는 경우)를 구분하여 차등적인 확률을 부여한다.

이 차등적인 확률은 하이퍼파라미터이며, 어떻게 부여했는지에 따라 다른 임베딩을 얻는다. 아래의 그림은 Node2Vec 방식으로 K-means 군집 분석을 수행한 결과이다.

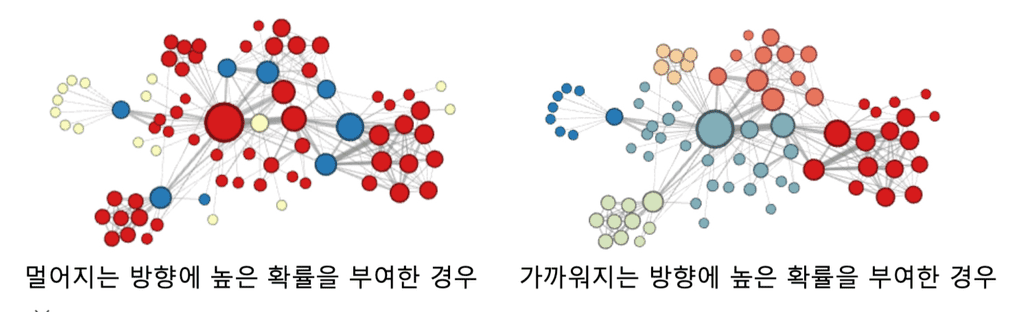
• 멀어지는 방향에 높은 확률을 부여하면, 정점의 '역할'(bridge 역할, 변두리 정점 등)이 같은 경우 임베딩이 유사해진다.
• 가까워지는 방향에 높은 확률을 부여하면, 같은 군집에 속한 정점들끼리 임베딩이 유사하게 나온다.

손실 함수 근사

랜덤 워크 기반의 손실함수는 정점의 수의 제곱에 비례하는 시간이 소요된다. 모든 시작점 각각에 대하여, 모든 도달점의 경우를 고려하기 때문이다.

이런 제곱합을 피하기 위해서 대부분 근사식을 사용하는데, 모든 정점에 대해 정규화하는 대신 몇개의 정점을 뽑아 비교하는 형태이다. 이 때 뽑힌 정점들을 Negative sample이라고 부른다.

• $\sigma$ : sigmoid 함수
• Negative sample의 숫자가 더 많을수록 학습이 안정적이다.

변환식 노드 임베딩과 귀납식 노드 임베딩

지금까지 언급한 노드 임베딩 방식들은 변환식(Transductive) 방법으로, 학습의 결과로 정점의 임베딩 값 자체를 출력값으로 얻는다.

그런데, 이런 변환식 방법에는 여러 한계가 있다.

• 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없다. 다시 학습을 수행해야한다.
• 모든 정점에 대한 임베딩을 미리 계산하여 저장해두고 꺼내 써야한다.
• 정점이 속성(Attribute) 정보를 가진 경우 이를 활용할 수 없다.

따라서 이런 한계점을 극복한 노드 임베딩 방식으로, 정점을 임베딩으로 변화시키는 '함수', 즉 인코더를 얻는 귀납식(Inductive) 방법이 나오게 되었다. 귀납식 노드 임베딩 방식의 대표적인 방식이 그래프 신경망(Graph Neural Network)이다.